Краткая теория

Лабораторная работа №5

Тема: Анализ и синтез сумматора с параллельным переносом.

Цель: синтезировать сумматор с параллельным переносом и проанализировать форму выходных сигналов.

Краткая теория.

В сумматоре с последовательным переносом тракты переносов всех одноразрядных сумматоров включены последовательно. Поэтому, даже при минимальной задержке тракта переноса одноразрядного сумматора в задержка n-разрядного сумматора не может быть менее . Для уменьшения задержки используется принцип параллельного переноса, когда входной перенос каждого разряда вырабатывается независимо от переноса соседнего младшего разряда. Он формируется как функция только слагаемых и входного переноса всего n-разрядного сумматора. Для всех разрядов сигналы переноса формируются параллельно.

Для описания работы сумматора с параллельным переносом удобно ввести две вспомогательные функции и , называемые иногда подготовительными:

- функция генерации переноса, CRG (от carry generation). Функция =1, когда слагаемые данного разряда таковы, что перенос в соседний старший разряд равен 1 независимо от значения входного переноса данного разряда, т.е. =1, если в данном разряде сумматора генерируется перенос в соседний старший разряд:

; (1)

- функция прозрачности, или распространения. Функция , когда слагаемые данного разряда таковы, что при переносе в данный разряд , равном 1, перенос в соседний старший разряд CR также равен 1, т.е. , если тракт переноса данного разряда сумматора прозрачен для сигнала переноса .

С помощью и можно представить работу тракта переноса одного разряда сумматора:

. (2)

Прозрачность разряда может быть может быть представлено двумя различными функциями:

. (3)

Значение CR в (2) будет одним тем же независимо от того, используется функция или . Эти функции имеют различные значения лишь при , а поскольку при таком сочетании слагаемых , то перенос CR равен 1 не зависимо от вида второго члена дизъюнкции (2)– или . Конкретная форма функции прозрачности выбирается разработчиком исходя из удобства ее реализации в используемом базисе.

Входным переносом первого разряда будет входной перенос всего n-разрядного сумматора

.

Входной перенос второго разряда будет равен 1, если слагаемые первого разряда и таковы, что в этом разряде генерируется перенос, или если на вход всего сумматора поступил перенос , а слагаемые и таковы, что первый разряд прозрачен по тракту переноса:

.

Аналогично рассуждая, можно прийти к выводу, что перенос на входе -го разряда сумматора должен быть равен 1, если перенос генерируется в -м разряде; или он генерируется в -м разряде, и при этом -й разряд прозрачен; или он генерируется в -м разряде, и при этом прозрачны разряды -й и –й; или …; или если на сумматор поступил входной перенос, и при этом прозрачный все разряды от 1-го по –й включительно;

. (4)

Полученные выражения можно представить в любом базисе: И-НЕ, И-ИЛИ-НЕ, ИЛИ-НЕ. В базисе И-НЕ, например, (4) представляется следующем образом:

. (5)

Трехразрядный сумматор, тракт параллельного переноса которого построен в соответствии с (5), показан на рис.1. Три блока в правой половине рисунка - это узлы сложения по модулю 2 трех аргументов: , и , вырабатывающие значение суммы данного разряда в соответствии с

.

Они могут быть построены и по любой другой подходящей схеме. Выходной перенос n-разрядного сумматора вырабатывается в последней секции блока параллельного переноса как перенос в очередной, -й разряд.

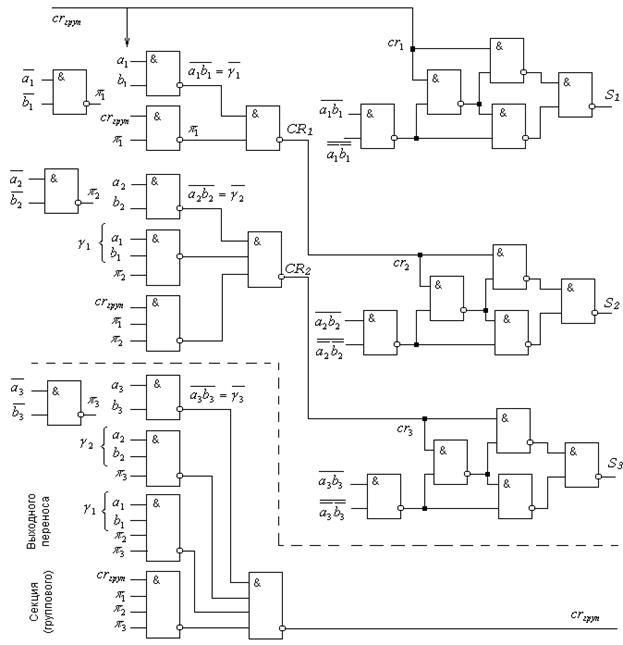
Рис.1. Трехразрядный сумматор с параллельным переносом.

Задержка Т получения суммы сумматора с параллельным переносом слагается из одинаковых для всех (кроме первого) разрядов задержки блока переноса– в зависимости от логического базиса и задержки трехвходовой схемы сложения по модулю 2- . От числа разрядов ни задержка получения суммы, ни задержка получения входного переноса не зависят. Аппаратурные затраты W сумматора с параллельным переносом заметно превышает W сумматора с последовательным переносом, и быстро растут с ростом разрядности.

Диапазон разрядности, в пределах которого сумматор с параллельным переносом эффективен, невелик. При малой разрядности – 2,3, даже 4 – он хуже сумматора с последовательным переносом и по W, и по T. Однако при каждом шаге увеличения разрядности на единицу также на единицу растет и требуемое число входов элементов И блока параллельного переноса. Поэтому, начиная с разрядности, примерно равной максимальному числу логических входов элементов используемой элементной базы, многовходовые И пришлось бы набирать, соединяя каскадом несколько маловходовых элементов. В принципе это возможно, но для схем сумматоров есть более эффективное решение. Поэтому разрядность реально используемых сумматоров с параллельным переносом сверху ограничивается максимальным числом входов элементов и редко превышает восемь. Параллельный перенос имеет 4-разрядный сумматор К155ИМ6, задержка которого примерно вдвое меньше тоже 4-разрядного К155ИМ3, но с последовательным переносом.