2015-06-26
1332
Метод Ньютона сводит решение нелинейной краевой задачи к решению серии линейных краевых задач и состоит в следующем.
Пусть для нелинейной краевой задачи (8.3) известна функция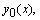 
удовлетворяющая граничным условиям и грубо приближенно равная искомому 
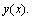Положим
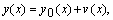(8.9)
где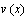 
— поправка к нулевому приближению 
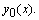Подставим (8.9) в уравнение (8.8) и линеаризуем задачу, используя следующие равенства:
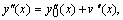
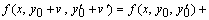
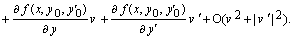
Отбрасывая остаточный член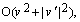 
получим линейную краевую задачу для нахождения поправки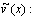 
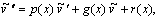
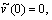
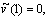(8.10)
где
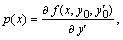
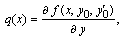
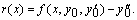
Решая линейную краевую задачу (8.10) каким-либо численным методом, найдем поправку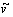 
и примем за первое приближение
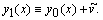
Аналогично, зная приближение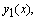 
положим 
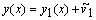и найдем следующее приближение. Продолжая процесс до тех пор, пока не будут выполнены неравенства
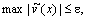
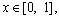
где e — требуемая точность, найдем приближенное решение исходной нелинейной задачи.
