Непрерывность отображения. Непрерывность числовой функции одной переменной, нескольких переменных.
Пусть функция y=f(x) определена в точке х0 и в некоторой окрестности
этой точки. Функция y=f(x) называется непрерывной в точке х0, если
существует предел функции в этой точке и он равен значению функции в этой
точке:
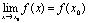
Это означает:
- функция определена в точке х0 и в ее окрестности;
- функция имеет предел при х→х0
- предел функции в точке х0 равен значению функции в этой точке, т.е.
выполняется равенство.
Это означает, что при нахождении предела непрерывной функции f(x) можно перейти
к пределу под знаком функции, то есть в функции f(x) вместо аргумента х
подставить предельное значение х0
Непрерывная функция — это непрерывное отображение, которое определено для числовых пространств.
Непрерывная числовая функция.
Положим, 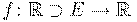 . (Вместо R, также допустимо использовать C.)
. (Вместо R, также допустимо использовать C.)
Функция f непрерывна в точке a, если для любого числа ε>0 найдётся такое число δ>0, что для всех точек 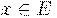 условие
условие 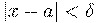 влечет
влечет 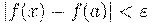 .
.
Или:
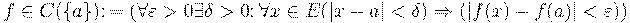 .
.
Если точка 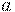 — предельная точка для множества
— предельная точка для множества 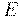 , то имеет смысл говорить о пределе функции
, то имеет смысл говорить о пределе функции 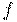 в данной точке
в данной точке 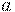 .
.
Другими словами, функция 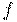 непрерывна в точке
непрерывна в точке 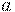 , предельной для множества
, предельной для множества 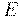 , если она имеет предел в данной точке и этот предел совпадает со значением функции в данной точке:
, если она имеет предел в данной точке и этот предел совпадает со значением функции в данной точке:
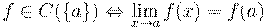
Функция 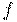 непрерывна на множестве
непрерывна на множестве 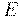 , если она непрерывна в каждой точке данного множества.
, если она непрерывна в каждой точке данного множества.
В этом случае говорят, что функция 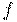 класса
класса 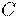 и пишут:
и пишут: 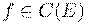 или, подробнее,
или, подробнее, 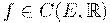 .
.
Неприрывное отображение из Rm в Rn
Обобщая одномерный случай, функция 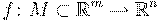 называется непрерывной в точке
называется непрерывной в точке 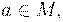 если
если 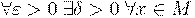
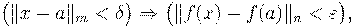
где
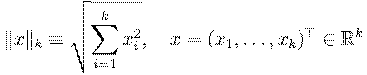 — евклидова норма в
— евклидова норма в 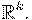
 2015-06-26
2015-06-26 1623
1623