Непрерывность функции на промежутке

Определение. Функция называется непрерывной на интервале, если она непрерывна в каждой точке этого интервала.

Если функция определена при х = а и при этом 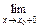f (х) = f (а),

то говорят, что f (х) в точке а непрерывна справа. Аналогично, если 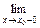f (х) = f (b), то говорят, что в точке b эта функция непрерывна слева.

Определение. Функция называется непрерывной на отрезке [ a, b ], если она непрерывна в каждой его точке (в точке а непрерывна справа, в точке b – непрерывна слева).

Наибольшим значением функции у = f (x) на отрезке [ a, b ] называется такое её значение f (x ₁), что f (x) £ f (x ₁) для всех х Î [ a, b ].

Наименьшим значением функции у = f (x) на отрезке [ a, b ] называется такое её значение f (x ₂), что f (x) ³ f (x ₂) для всех х Î [ a, b ].

Функции, непрерывные на отрезке, обладают рядом важных свойств, которые выражаются следующими теоремами.

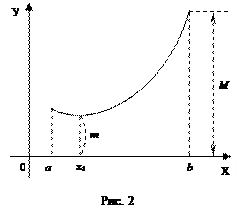
Теорема 3.3.1. Функция, непрерывная на отрезке [ a, b ], достигает на нём своего наименьшего значения m и наибольшего значения M, то есть существуют такие точки x ₁ и x ₂ этого отрезка, что f (x ₁) = m, f (x ₂) = M.

Теорема имеет простой геометрический смысл (см. рис.2).

Теорема 3.3.2. Если функция у = f (x) непрерывна на отрезке [ a, b ] и на его концах принимает неравные значения f (а) = А, f (b) = В, А ¹ В, то каково бы ни было число С, заключённое между А и В, найдётся точка с Î [ a, b ] такая, что f (с) = С.

Геометрический смысл теоремы иллюстрируется на рис.3. Всякая прямая у = С, где A < C < B (или A > C > B), пересекает график функции у = f (x).

Следствие. Если функция непрерывна на отрезке и на его концах принимает значения разных знаков, то на этом отрезке найдётся хотя бы одна точка, в которой функция обращается в нуль.

Геометрический смысл следствия иллюстрируется на рис.4.

Вопросы для самоконтроля

1. Какая функция называется непрерывной в точке?

2. Приведите еще одно эквивалентное определение через приращение функции и аргументов.

3. Что можно сказать о сумме, разности, произведении и частном двух непрерывных функций?

4. При каких значениях аргумента целая рациональная и дробно-рациональная функции непрерывны?

5. Когда сложная функция непрерывна в точке?

6. Что называется точкой разрыва функций?

7. Какие точки называются точками разрыва первого рода?

8. Какая величина называется скачком функции?

9. Разъясните понятия ''точка устранимого разрыва''. Приведите примеры.

10. Какие точки называются точками разрыва второго рода? Приведите примеры.

11. Разъясните понятия: ''непрерывность на интервале'', ''непрерывность справа'', ''непрерывность слева'', ''непрерывность на отрезке''.

12. Дайте определение наибольшего и наименьшего значения функций.

13. Сформулируйте теорему о связи непрерывности на отрезке с наибольшим и наименьшим значениями функции. Разъясните ее на рисунке.

14. Сформулируйте теорему о связи непрерывности функций на отрезке с отрезком значений функций. Проиллюстрируйте ее геометрический смысл на рисунке.

15. Приведите следствие из вышеуказанной теоремы и его геометрическую интерпретацию.

ЛЕКЦИЯ №4

Тема лекции: Производная функции

План лекции: Понятие производной, её геометрический и физический смысл. Основные правила дифференцирования. Производная сложной функции. Некоторые приложения производной.

4.1. Понятие производной, её геометрический и физический смысл

Рассмотрим функцию у = f (x), заданную в интервале ] a, b [. Пусть х 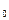Î ] a, b [ и х Î ] a, b [, тогда приращение функции в точке х ₀ выражается формулой D у = f (x ₀ + D х) – f (x ₀).

Определение. Производной функции у = f (x) в точке х ₀ называется предел отношения приращения этой функции к приращению аргумента, когда последнее стремится к нулю:

f’ (x ₀) = 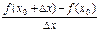или y' (x ₀) =.

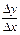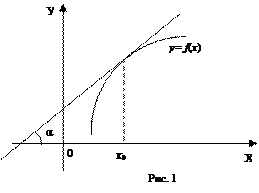
Геометрический смысл производной: производная от данной функции в точке равна тангенсу угла между осью Ох и касательной к графику этой функции в соответствующей точке (см. рис.1):

f' (x ₀) = tg a.

Уравнение касательной к линии у = f (x) в точке М₀(х ₀, у ₀) имеет вид

у – у ₀ = f' (x ₀)(х – х ₀).

Физический смысл производной: производная от пути по времени равна скорости прямолинейного движения точки: х' (t ₀) = v.

Функция, имеющая производную в данной точке, называется дифференцируемой в данной точке. Функция, имеющая производную в каждой точке данного промежутка, называется дифференцируемой в

этом промежутке. Операция нахождения производной называется дифференцированием.

Зависимость между непрерывностью и дифференцируемостью функции выражается следующей теоремой.

Теорема 4.1.1. Если функция у = f (x) дифференцируема в данной точке, то она непрерывна в ней.

Доказательство. Пусть функция у = f (x) дифференцируема в точке х ₀, то есть существует предел y' (х ₀) =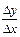. Так как D у = 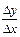×D х, то

D у = 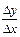×D х = y' (х ₀)×0 = 0, т.е. D у = 0.

Теорема доказана.