Функции комплексного переменного
Пусть комплексное переменное z = x + yi принимает всевозможные значения из некоторого множества Z.
Если каждому значению z из Z можно поставить в соответствие одно или несколько значений другого комплексного переменного w = u + vi, то комплексное переменное w называют функцией от z в области Z и пишут w = f (z).
Функция w = f (z) называется однозначной, если каждому значению z из множества Z можно поставить в соответствие только одно значение w. Если же существуют значения z, каждому из которых можно поставить в соответствие несколько значений w, то функция w = f (z) называется многозначной.
Если w = u + vi есть функция от z = x + yi, то каждое из переменных u и v является действительной функцией от х и у, т.е. w = u (х, у) + v (х, у) i.
Однозначная функция w = f (z) при z → с имеет конечный предел С (с и С – комплексные числа), если для любого сколь угодно малого числа ε > 0 найдётся такое число δ > 0, что из неравенства | z – c | < δ следует неравенство | f (z) – С | < ε.
В этом случае пишут
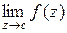 = С.
= С.
Функция w = f (z) называется непрерывной в точке z 0, если 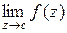 = f (z 0). Функция, непрерывная в любой точке некоторой области D называется непрерывной в этой области.
= f (z 0). Функция, непрерывная в любой точке некоторой области D называется непрерывной в этой области.
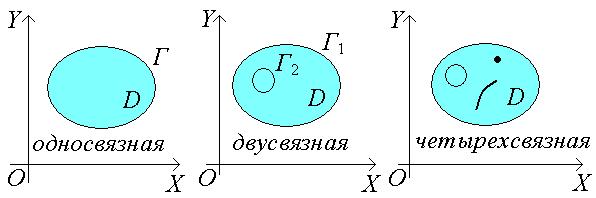
Область D, ограниченная замкнутой не самопересекающейся линией Г, называется односвязной.
Если же область D, ограничена двумя замкнутыми не пересекающимися и не самопересекающимися линиями Г 1 и Г 2, то область D называется двусвязной и т.д.
Функции комплексного переменного еz, 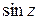 ,
, 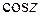 ,
, 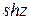 ,
, 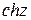 определяются как суммы следующих рядов, сходящихся во всей плоскости комплексного переменного:
определяются как суммы следующих рядов, сходящихся во всей плоскости комплексного переменного:
еz = 1 + 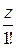 +
+ 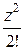 +
+ 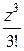 + …,
+ …,
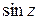 =
= 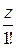 −
− 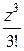 +
+ 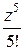 − …,
− …,
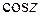 = 1 −
= 1 − 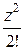 +
+ 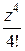 −
− 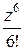 + …,
+ …,
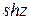 =
= 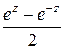 =
= 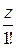 +
+ 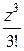 +
+ 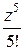 + …,
+ …,
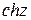 =
= 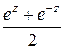 = 1 +
= 1 + 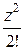 +
+ 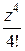 +
+ 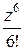 + ….
+ ….
Для функции комплексного переменного справедлива формула Эйлера:
еzi = 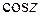 + i
+ i 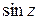 .
.
Из этой формулы следуют следующие формулы:
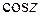 =
= 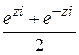 ,
, 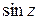 =
= 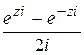 .
.
Отметим ещё две формулы:
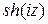 = i
= i 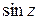 ,
, 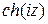 =
= 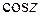 .
.
Известные из элементарной математики формулы справедливы и для комплексных значений аргументов z 1 и z 2:
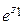 ∙
∙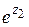 =
= 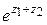 ,
, 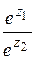 =
= 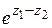 ,
,
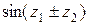 =
= 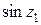
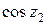 ±
± 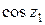
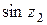 ,
,
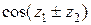 =
= 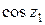
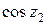
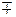
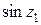
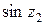 .
.
Функции 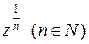 ,
, 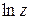 ,
, 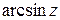 ,
, 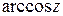 ,
, 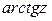 определяются как обратные по отношению соответственно к функциям
определяются как обратные по отношению соответственно к функциям 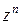 ,
, 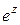 ,
, 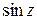 ,
, 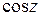 ,
, 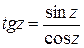 . При этом функции
. При этом функции 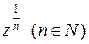 ,
, 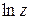 ,
, 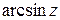 ,
, 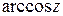 ,
, 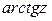 являются многозначными.
являются многозначными.
Можно показать, что
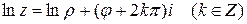 ,
,
где 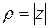 и
и 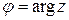 .
.
Пример. Дана функция 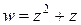 . Найти значение функции при
. Найти значение функции при 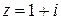 .
.
□ Имеем 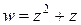 =
= 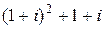 =
= 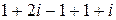 =
= 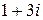 . ■
. ■
Пример. Дана функция 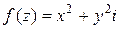 , где
, где 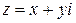 . Найти
. Найти 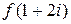 .
.
□ Имеем 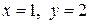 , Следовательно,
, Следовательно, 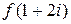 =
= 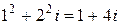 . ■
. ■
Пример. Найти 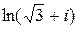 .
.
□ Имеем 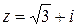 ,
, 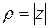 = 2,
= 2, 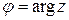 =
= 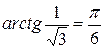 , т.е.
, т.е.
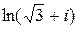 =
= 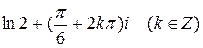 . ■
. ■
Пример. Вычислить 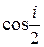 с точностью
с точностью 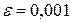 .
.
□ Так как
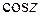 = 1 −
= 1 − 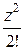 +
+ 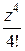 −
− 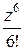 + …,
+ …,
то 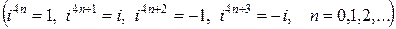
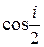 = 1 +
= 1 + 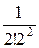 +
+ 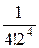 +
+ 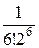 + …
+ … 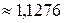 .
.
Три знака после запятой гарантированы. ■
Производная функции комплексного переменного
Производной однозначной функции комплексного переменного w = f (z) называется предел
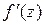 =
=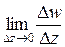 =
=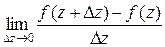 .
.
Функция, имеющая производную при данном значении z, называется дифференцируемой (моногенной) при этом значении z.
Если функция w = f (z) однозначна и имеет конечную производную в каждой точке области D, то она называется аналитической в этой области D.
Если функция w = f (z) = u (х, у) + v (х, у) i дифференцируема в точке z = x + yi, то в этой точке существуют частные производные 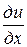 ,
, 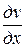 ,
, 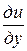 ,
, 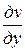 , причем эти производные связаны условиями
, причем эти производные связаны условиями
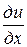 =
= 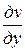 ,
, 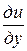 = −
= − 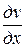 ,
,
которые называются условиями Коши−Римана.
Условия Коши – Римана являются необходимыми условиями дифференцируемости функции w = f (z) в точке z = x + yi.
Обратно, если частные производные 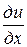 ,
, 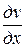 ,
, 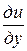 ,
, 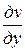 непрерывны в точке z = x + yi и условия Коши – Римана
непрерывны в точке z = x + yi и условия Коши – Римана 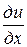 =
= 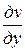 ,
, 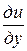 = −
= − 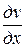 выполнены, то функция w = f (z) дифференцируема в точке z = x + yi.
выполнены, то функция w = f (z) дифференцируема в точке z = x + yi.
Производная функции f (z) выражается через частные производные функций u (х, у) и v (х, у) по формулам:
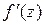 =
= 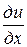 + i
+ i 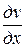 =
= 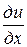 − i
− i 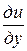 =
= 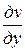 − i
− i 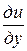 =
= 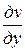 + i
+ i 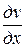 .
.
Производные элементарных функций zn, еz, 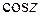 ,
, 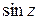 ,
, 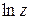 ,
, 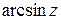 ,
, 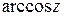 ,
, 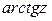 ,
, 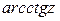 ,
, 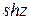 ,
, 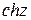 находятся по тем же формулам, что и для действительного аргумента. Отметим только, что
находятся по тем же формулам, что и для действительного аргумента. Отметим только, что
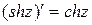 ,
, 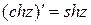 .
.
Пример. Дифференцируема ли функция f (z) = у + хi?
□ Имеем и = у, v = x. Проверим выполнения условий Коши – Римана 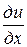 =
= 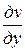 ,
, 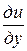 = −
= − 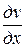 . Находим
. Находим 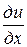 = 0,
= 0, 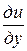 = 1,
= 1, 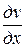 = 1,
= 1, 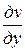 = 0, Видно, что
= 0, Видно, что 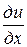 =
= 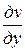 , но
, но 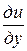
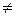 −
− 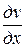 . Следовательно, данная функция не является дифференцируемой. ■
. Следовательно, данная функция не является дифференцируемой. ■
Пример. Дифференцируема ли функция f (z) = 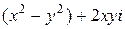 ?
?
□ Имеем и = 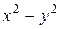 , v =
, v = 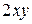 ,
, 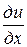 = 2 х,
= 2 х, 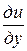 = − 2 у,
= − 2 у, 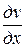 = 2 у,
= 2 у, 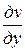 = 2 х. Условия Коши – Римана
= 2 х. Условия Коши – Римана 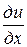 =
= 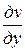 ,
, 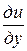 = −
= − 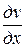 выполняются. Следовательно, функция дифференцируема. Так как
выполняются. Следовательно, функция дифференцируема. Так как 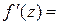
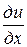 + i
+ i 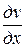 , то
, то
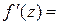 2 х + 2 уi =
2 х + 2 уi = 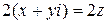 .
.
Производную можно было найти иначе:
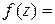
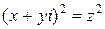 ,
, 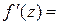
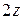 . ■
. ■
Пример. Дана действительная часть 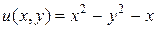 дифференцируемой функции
дифференцируемой функции  , где z = x + yi. Найти функцию
, где z = x + yi. Найти функцию  .
.
□ Имеем 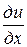 = 2 х – 1. Так как
= 2 х – 1. Так как 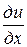 =
= 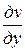 (одно из условий Коши – Римана), то
(одно из условий Коши – Римана), то 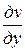 = 2 х – 1. Интегрируя, находим
= 2 х – 1. Интегрируя, находим
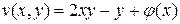 ,
,
где 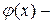 произвольная функция.
произвольная функция.
Используем второе условие Коши – Римана: 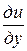 = −
= − 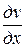 . Так как
. Так как 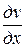 =
= 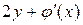 , то
, то 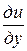 =
=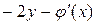 . Но из условия задачи находим, что
. Но из условия задачи находим, что 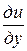 =
= 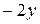 . Следовательно,
. Следовательно,
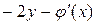 =
= 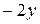 ,
, 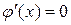 ,
, 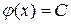 .
.
Тогда
 =
= 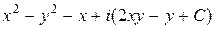 =
= 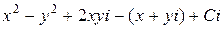
или
 =
= 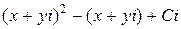 , т.е.
, т.е.  =
= 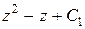 . ■
. ■
Интеграл от функции комплексного переменного
Кривая Г называется гладкой, если она имеет непрерывно изменяющуюся касательную.
Кривая называется кусочно-гладкой, если она состоит из конечного числа гладких дуг.
Пусть дана функция комплексного переменного w = f (z), непрерывная в некоторой области D. Пусть Г – произвольная гладкая кривая, лежащая в области D. Рассмотрим дугу кривой с началом в точке z 0 и концом в точке z. Разделим эту дугу на п частей произвольными точками z 0, z 1, z 2, …, 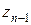 , zп = z, расположенными последовательно на линии Г.
, zп = z, расположенными последовательно на линии Г.
Составим сумму
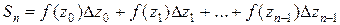 ,
,
где 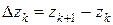
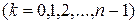 . Пусть
. Пусть 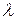 − наибольшая из величин
− наибольшая из величин 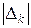 . Если
. Если 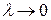 , то
, то 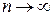 и сумма
и сумма 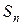 стремится к определенному пределу. Этот предел называется интегралом функции f (z) по дуге кривой Г, заключенной между точками z 0 и z, т.е.
стремится к определенному пределу. Этот предел называется интегралом функции f (z) по дуге кривой Г, заключенной между точками z 0 и z, т.е.
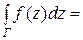
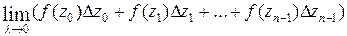 .
.
Если f (z) = u (х, у) + i v (х, у), то 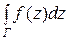 сводится к двум криволинейным интегралам от действительных функций:
сводится к двум криволинейным интегралам от действительных функций:
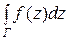 =
= 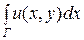 − v (х, у) dy + i
− v (х, у) dy + i 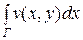 + u (х, у) dy.
+ u (х, у) dy.
Пусть Г – кусочно-гладкая функция, состоящая из гладких частей Г 1, Г 2, …, Гт. Тогда
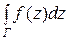 =
= 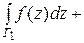
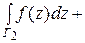 … +
… +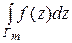 .
.
Если f (z) – аналитическая функция в односвязной области D, то значение интеграла 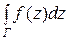 , взятого вдоль произвольной кусочно-гладкой линии Г, принадлежащей области D, не зависит от линии Г, а определяется лишь положениями начальной и конечной точек этой линии.
, взятого вдоль произвольной кусочно-гладкой линии Г, принадлежащей области D, не зависит от линии Г, а определяется лишь положениями начальной и конечной точек этой линии.
Теорема Коши. Для всякой аналитической функции f (z) в некоторой односвязной области D интеграл 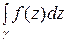 , взятый по любому замкнутому кусочно-гладкому контуру
, взятый по любому замкнутому кусочно-гладкому контуру 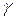 , лежащему в области D, равен нулю.
, лежащему в области D, равен нулю.
Так же как и для действительных функций, справедлива формула
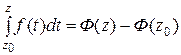
(формула Ньютона – Лейбница), где Ф (z) – какая-нибудь первообразная функция по отношению к f (z).
Для нахождения первообразной функции по отношению к аналитической функции f (z) применяются обычные формулы интегрирования.
Рассмотрим п + 1 замкнутых кусочно-гладких линий 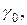
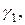
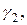 …,
…, 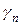 таких, что каждая из линий
таких, что каждая из линий 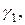
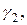 …,
…, 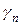 лежит вне остальных и все они расположены внутри
лежит вне остальных и все они расположены внутри 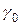 . Множество точек, лежащих одновременно внутри
. Множество точек, лежащих одновременно внутри 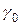 и вне
и вне 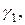
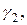 …,
…, 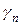 , представляет собой (п + 1)-связную область D.
, представляет собой (п + 1)-связную область D.
Пусть f (z) – аналитическая функция в области D (включая значения на контурах 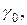
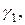
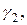 …,
…, 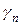 ). Тогда
). Тогда
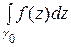 =
= 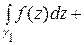
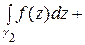 … +
… +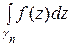 .
.
Пример. Вычислить интеграл
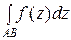 ,
,
где 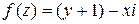 , АВ – отрезок прямой, соединяющий точки
, АВ – отрезок прямой, соединяющий точки 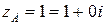 ,
, 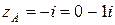 .
.
□ Имеем 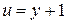 ,
, 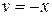 . Отсюда
. Отсюда
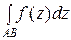 =
= 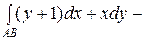
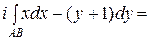
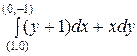 −
−
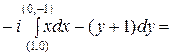
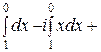
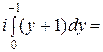
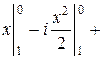
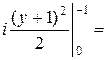
= 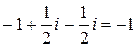 .
.
Интеграл можно найти по-другому. Видно, что 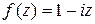 (
(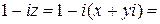
=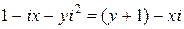 ). Тогда
). Тогда
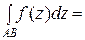
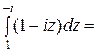
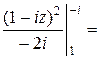
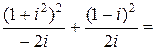
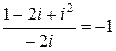 . ■
. ■
Пример. Вычислить интеграл
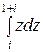 .
.
□ Подынтегральная функция аналитическая. Используя формулу Ньютона – Лейбница, получим
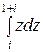 =
= 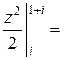
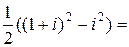
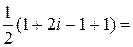
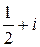 . ■
. ■
Ряды Тейлора и Лорана
Пусть дана функция  , аналитическая в некоторой окрестности точки а.
, аналитическая в некоторой окрестности точки а.
Ряд
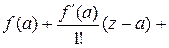
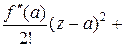
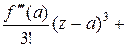 …
…
называе5тся рядом Тейлора функции  и внутри своего круга сходимости выражает функцию
и внутри своего круга сходимости выражает функцию  , т.е.
, т.е.
 =
= 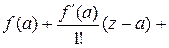
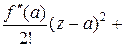
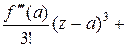 ….
….
Если а = 0, то
 =
= 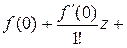
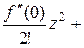
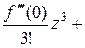 ….
….
В этом случае говорят, что функция  разложена в ряд Маклорена.
разложена в ряд Маклорена.
Рассмотрим два ряда
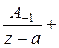
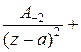
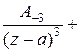 … (1)
… (1)
и
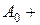
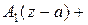
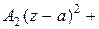
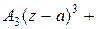 …. (2)
…. (2)
Область сходимости ряда (1) (если она существует) определяется неравенством 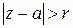 . Если существует область сходимости ряда (2), то она определяется неравенством
. Если существует область сходимости ряда (2), то она определяется неравенством 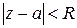 . Тогда при условии r < R для ряда
. Тогда при условии r < R для ряда
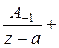
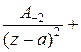
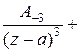
+ 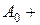
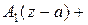
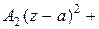
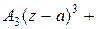 …
…
областью сходимости служит кольцо 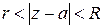 , ограниченное концентрическими окружностями с центром в точке а и радиусами r и R.
, ограниченное концентрическими окружностями с центром в точке а и радиусами r и R.
Пусть  − однозначная и аналитическая функция в кольце
− однозначная и аналитическая функция в кольце 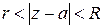 . Эта функция в указанном кольце может быть представлена в виде
. Эта функция в указанном кольце может быть представлена в виде
 =
= 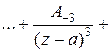
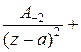
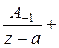
+ 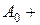
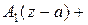
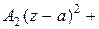
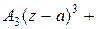 ….
….
Ряд в правой части равенства называется рядом Лорана функции  . Коэффициенты этого ряда можно вычислить по формуле
. Коэффициенты этого ряда можно вычислить по формуле
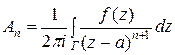
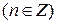 .
.
Ряд (1) называется главной частью ряда Лорана, а ряд (2) – правильной частью ряда Лорана.
Особые точки. Если функция  − аналитическая функция в окрестности точки а, то характер этой точки определяется по виду разложения функции в ряд Лорана в окрестности точки а следующим образом:
− аналитическая функция в окрестности точки а, то характер этой точки определяется по виду разложения функции в ряд Лорана в окрестности точки а следующим образом:
1). Если ряд Лорана не содержит главной части. Тогда имеем устранимую особую точку а. В этом случае существует конечный предел 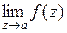 .
.
2). Если ряд Лорана содержит конечное число п членов главной части, то точка а является полюсом п - го порядка. В этом случае  − аналитическая функция в окрестности точки а и стремится к бесконечности при
− аналитическая функция в окрестности точки а и стремится к бесконечности при 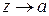 .
.
3). Если ряд Лорана содержит бесконечное число членов главной части, то точка а является существенно особой точкой. В этом случае при 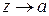 функция
функция  не имеет предела, т.е. предел не существует.
не имеет предела, т.е. предел не существует.
В случаях 2) и 3) коэффициент 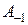 в ряде Лорана называется вычетом функции
в ряде Лорана называется вычетом функции  в точке
в точке 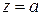 .
.
Между нулем и полюсом функции существует связь. Если 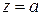 − ноль кратности k функции
− ноль кратности k функции  , то
, то 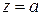 − полюс того же порядка функции
− полюс того же порядка функции 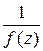 ; обратно, если
; обратно, если 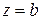 − полюс порядка k функции
− полюс порядка k функции  , то
, то 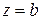 − ноль функции
− ноль функции 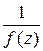 .
.
Следует отметить, что если 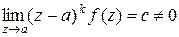 , то
, то 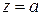 − полюс порядка k функции
− полюс порядка k функции  .
.
Пример. Разложить в ряд Тейлора по степеням бинома 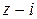 функцию
функцию  =
= 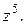
□ Находим производные функции  =
= 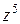 :
: 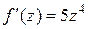 ,
,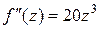 ,
, 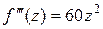 ,
,
f ІV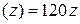 , f V
, f V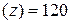 , f VІ
, f VІ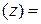 f VІІ
f VІІ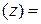 …=0.
…=0.
Определяем значения производных в точке 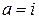 :
: 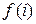 =
= 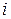 ,
, 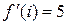 ,
, 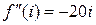 ,
, 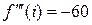 , f ІV
, f ІV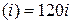 , f V
, f V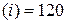 .
.
Отсюда
 =
= 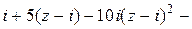
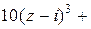
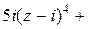
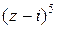 .
.
Рядом Тейлора функции  =
= 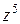 является многочлен пятой степени. ■
является многочлен пятой степени. ■
Пример. Разложить в ряд Лорана по степеням 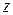 функцию
функцию  =
= 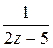 в окрестности точки
в окрестности точки 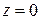 ,
,
□ Представим данную функцию в виде
 =
= 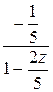 .
.
В окрестности точки 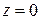 выполняется неравенство
выполняется неравенство 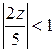 , поэтому дробь
, поэтому дробь 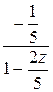 можно рассматривать как сумму бесконечно убывающей геометрической прогрессии с первым членом и =
можно рассматривать как сумму бесконечно убывающей геометрической прогрессии с первым членом и = 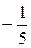 и знаменателем
и знаменателем 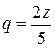 . Отсюда получаем
. Отсюда получаем
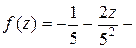
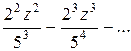 или
или 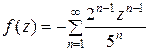 .
.
Это разложение содержит только правильную часть. Из неравенства 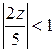 следует, что областью сходимости ряда является круг
следует, что областью сходимости ряда является круг 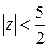 . ■
. ■
Пример. Разложить в ряд Лорана функцию  =
= 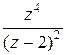 в по степеням
в по степеням 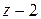 .
.
□ Положим 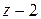 =
= 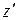 . Тогда
. Тогда
 =
= 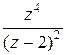 =
= 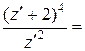
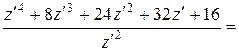
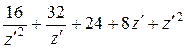 ,
,
т.е.
 =
= 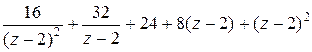 .
.
Здесь главная часть содержит два члена, а правильная – три члена. Так как разложение содержит конечное число членов, то оно справедливо для любой точки плоскости, кроме 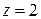 . Эта точка является полюсом второго порядка функции
. Эта точка является полюсом второго порядка функции  . Вычетом этой функции относительно полюса
. Вычетом этой функции относительно полюса 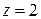 является коэффициент при
является коэффициент при 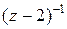 , т.е. 32. ■
, т.е. 32. ■
Вычисление вычетов функции. Применение вычетов к вычислению интегралов
Пусть а – полюс п -го порядка функции  . Вычет функции
. Вычет функции  относительно ее полюса п -го порядка вычисляется по формуле
относительно ее полюса п -го порядка вычисляется по формуле
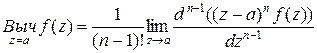 .
.
Если а – полюс первого порядка (простой полюс) функции  , то
, то
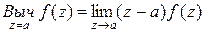 .
.
Если функция  =
=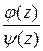 , где
, где 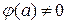 , а
, а 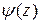 имеет простой ноль при
имеет простой ноль при 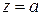
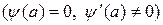 , то
, то 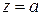 является простым полюсом и справедлива формула
является простым полюсом и справедлива формула
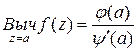 .
.
Теорема (основная теорема о вычетах). Пусть  − аналитическая функция в замкнутой области D, кроме конечного числа особых точек а 1, а 2, а 3, …, аk (полюсов или существенно особых точек). Тогда интеграл от функции по контуру
− аналитическая функция в замкнутой области D, кроме конечного числа особых точек а 1, а 2, а 3, …, аk (полюсов или существенно особых точек). Тогда интеграл от функции по контуру 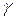 , содержащему внутри себя эти точки и целиком лежащему в области D, равен произведению 2
, содержащему внутри себя эти точки и целиком лежащему в области D, равен произведению 2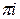 на сумму вычетов в указанных особых точках, т.е.
на сумму вычетов в указанных особых точках, т.е.
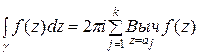 .
.
Частный случай. Пусть  − аналитическая функция в замкнутой области D, число а принадлежит области D и
− аналитическая функция в замкнутой области D, число а принадлежит области D и 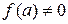 . В этом случае функция
. В этом случае функция 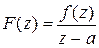 имеет в области D полюс а первого порядка. Найдем вычет функции
имеет в области D полюс а первого порядка. Найдем вычет функции 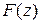 относительно полюса а:
относительно полюса а:
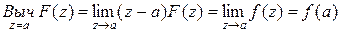 .
.
Отсюда, применяя основную теорему о вычетах, получим
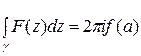
или
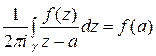
− формула Коши.
Пусть  − аналитическая функция в верхней полуплоскости, включая действительную ось, за исключением конечного числа полюсов
− аналитическая функция в верхней полуплоскости, включая действительную ось, за исключением конечного числа полюсов 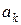
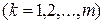 , расположенных над действительной осью. Кроме того, предполагается, что произведение
, расположенных над действительной осью. Кроме того, предполагается, что произведение 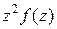 при
при 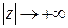 имеет конечный предел. В этом случае для вычисления определенного интеграла
имеет конечный предел. В этом случае для вычисления определенного интеграла 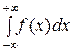 функции действительного переменного применяется формула
функции действительного переменного применяется формула
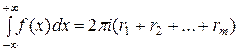 ,
,
где 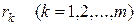 − вычет функции
− вычет функции  относительно полюса
относительно полюса 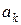 .
.
Пример. Найти вычеты функции  =
=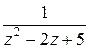 .
.
□ Простыми полюсами функции являются корни знаменателя 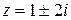 . Следовательно,
. Следовательно,  =
=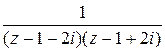 . Находим
. Находим
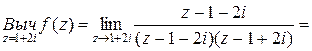
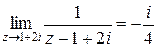 ,
,
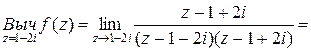
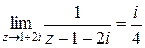 . ■
. ■
Пример. Найти вычеты функции  =
=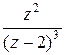 .
.
□ Так как 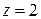 − полюс третьего порядка, то
− полюс третьего порядка, то
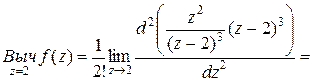
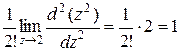 . ■
. ■
Пример. Найти 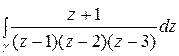 , где
, где 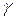 − замкнутый контур, внутри которого находятся полюсы
− замкнутый контур, внутри которого находятся полюсы 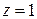 ,
, 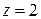 ,
, 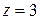 .
.
□ Определяем вычеты подынтегральной функции:
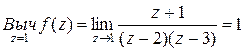 ,
, 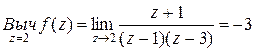 ,
,
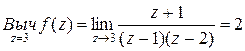 .
.
Следовательно,
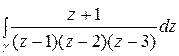 =
= 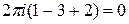 . ■
. ■
Пример. Вычислить определенный интеграл 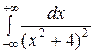 .
.
□ Функция 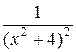 является аналитической в верхней полуплоскости, за исключением полюса
является аналитической в верхней полуплоскости, за исключением полюса 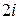 . Кроме того,
. Кроме того,
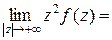
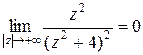 ,
,
т.е. является конечной величиной.
Найдем вычет функции 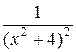 относительно полюса второго порядка
относительно полюса второго порядка 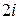 :
:
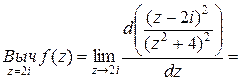
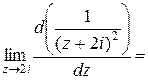
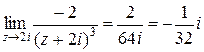 .
.
Следовательно,
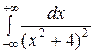 =
= 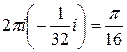 . ■
. ■
 2014-02-09
2014-02-09 2418
2418
