Раздел 1. Элементы линейной и векторной алгебры

Задания 1─10. 1. Исследовать систему линейных уравнений.

2. В случае совместности, решить систему методом Гаусса.

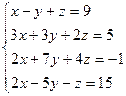
1.	2.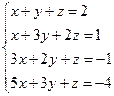
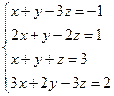
3.	4.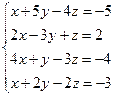
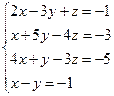
5.	6.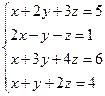
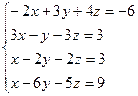
7.	8.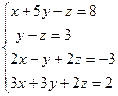
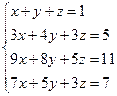
9.	10.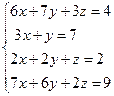

Задания 11─20. Даны векторы

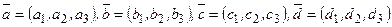
в некотором базисе. Показать, что векторы 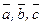образуют базис и найти координаты вектора 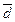в этом базисе. Систему линейных уравнений решить по формулам Крамера.

11. 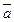= (1; 2; 3), 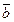= (-1; 3; 2), 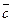= (7; -3; 5),

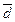= (6; 10; 17).

12. 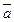= (4; 7; 8), 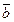= (9; 1; 3), 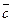= (2; -4; 1),

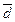= (1; -13; -13).

13. 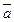= (8; 2; 3), 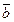= (4; 6; 10), 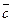= (3; -2; 1),

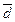= (7; 4; 11).

14. 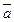= (10; 3; 1), 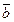= (1; 4; 2), 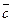= (3; 9; 2),

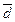= (19; 30; 7).

15. 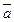= (2; 4; 1), 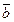= (1; 3; 6), 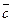= (5; 3; 1),

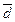= (24; 20; 6).

16. 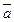= (1; 7; 3), 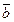= (3; 4; 2), 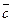= (4; 8; 5),

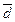= (7; 32; 14).

17. 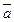= (1; -2; 3), 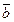= (4; 7; 2), 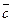= (6; 4; 2),

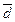= (14; 18; 6).

18. 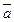= (1; 4; 3), 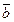= (6; 8; 5), 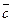= (3; 1; 4),

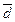= (21; 18; 33).

19. 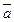= (2; 7; 3), 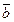= (3; 1; 8), 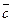= (2; -7; 4),

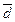= (16; 14; 27).

20. 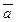= (7; 2; 1), 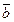= (4; 3; 5), 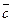= (3; 4; -2),

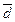= (2; -5; -13).