Неравномерное распределение напряжений

Многие элементы строений и детали машин нагружаются так, что напряжения во всех их поперечных сечениях распределены неравномерно. Чтобы вывести формулы для расчета напряжений в таких условиях, мысленно разрезают элемент плоскостью, которая дает нужное поперечное сечение, на две части и рассматривают условия равновесия одной из них. На эту часть действуют одна или несколько заданных внешних сил, а также силы, эквивалентные напряжениям в данном поперечном сечении. Действующие напряжения должны удовлетворять условиям равновесия и соответствовать деформациям. Эти два требования составляют основу для решения задачи. Второе из них подразумевает справедливость закона Гука. Типичными элементами с неравномерным распределением напряжений являются нагруженные балки, валы под действием скручивающих сил, растянутые или сжатые стержни с дополнительным изгибом и колонны.

БАЛКИ

Балка – это длинный стержень с опорами и нагрузками, работающий в основном на изгиб. Поперечное сечение балки обычно одинаково по всей ее длине. Силы, с которыми опоры действуют на балку, называются реакциями опор. Наиболее распространены два вида балок: консольная (рис. 5, а) и балка с двумя опорами, называемая простой (рис. 5, б). Под действием нагрузок балка прогибается. При этом «волокна» на ее верхней стороне сокращаются, а на нижней – удлиняются. Очевидно, что где-то между верхней и нижней сторонами балки имеется тонкий слой, длина которого не изменяется. Он называется нейтральным слоем. Изменение длины волокна, расположенного между верхней (или нижней) стороной балки и ее нейтральным слоем, пропорционально расстоянию до нейтрального слоя. Если справедлив закон Гука, то напряжения тоже пропорциональны этому расстоянию.

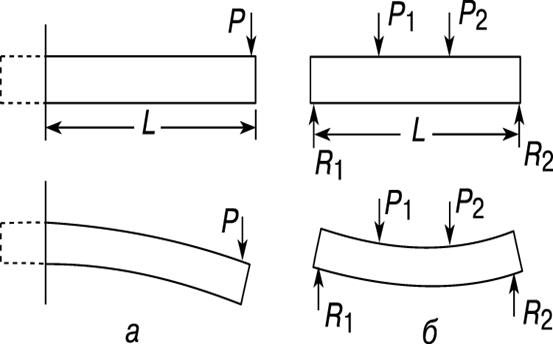
Рис. 5. ДВА ТИПА БАЛОК: а – консольная, б – простая. P, P 1 и P 2 – сосредоточенные нагрузки; R 1 и R 2 – реакции опор; L – длина.

Формула изгиба. На основе указанного распределения напряжений, дополненного условиями статики, выведена т.н. формула изгиба, в которой напряжение выражается через нагрузки и размеры балки. Она обычно представляется в виде^

σ = Mc / I,

где σ – максимальное напряжение в рассматриваемом поперечном сечении, c – расстояние от нейтрального слоя до наиболее напряженного волокна, M – изгибающий момент, равный сумме моментов всех сил, действующих по одну сторону от этого сечения, а I – момент инерции поперечного сечения (определенная функция формы и размеров последнего). Характер изменения нормальных напряжений в поперечном сечении балки показан на рис. 6.

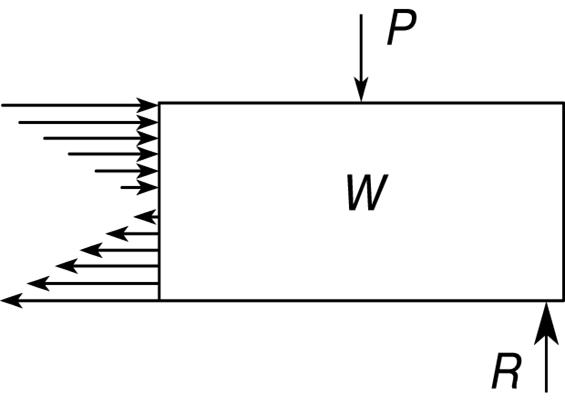
Рис. 6. РАСПРЕДЕЛЕНИЕ НОРМАЛЬНЫХ НАПРЯЖЕНИЙ в поперечном сечении балки. P – нагрузка, R – реакция, W – вес (распределенная нагрузка).

В поперечных сечениях балок действуют также касательные напряжения. Их вызывает равнодействующая всех вертикальных сил, приложенных по одну сторону поперечного сечения горизонтальной балки. Сумма всех внешних сил и реакций, действующих на одну из двух частей балки, называется сдвигом в сечении балки и обычно обозначается через V. Касательные напряжения неравномерно распределены по сечению: они равны нулю на верхнем и нижнем краях сечения и почти всегда максимальны в нейтральном слое.

Прогиб балки. Часто требуется рассчитать прогиб балки, вызванный действием нагрузки, т.е. вертикальное смещение точки, лежащей в нейтральном слое. Это очень важная задача, поскольку прогиб и кривизну балки нужно знать при решении задач, относящихся к широкому кругу т.н. статически неопределимых систем.

Еще в 1757 году Л.Эйлер вывел формулу для кривизны изогнутой балки. В этой формуле кривизна балки выражается через переменный изгибающий момент. Чтобы найти ординату упругой кривой (прогиб), необходимо брать двойной интеграл. В 1868 году О.Мор (Германия) предложил метод, основанный на эпюрах изгибающих моментов. Этот графоаналитический метод имеет огромное преимущество перед прежними методами, так как позволяет свести все математические вычисления к сравнительно простым арифметическим выкладкам. Он дает возможность вычислять прогиб и наклон в любой точке балки при любой нагрузке.

Статически неопределимые балки. Многие балки, используемые в строениях и машинах, имеют более двух опор или только две опоры, но с заделкой одного из концов, исключающей возможность поворота. Такие балки называются статически неопределимыми, поскольку уравнений статики недостаточно для определения реакций в опорах и моментов в заделке. Чаще всего рассматриваются подобные балки трех типов: с одним заделанным (защемленным) концом и одной опорой, с заделанными обоими концами и неразрезные балки, имеющие более двух опор (рис. 7).

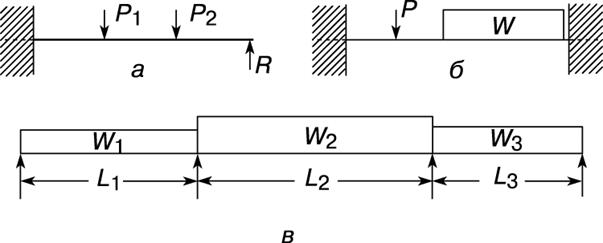
Рис. 7. СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ БАЛКИ: а – с одним заделанным концом; б – с двумя заделанными концами; в – неразрезная трехпролетная. P, P ₁, P ₂ – сосредоточенные нагрузки; R – реакция; L ₁, L ₂, L ₃ – длины; W, W ₁, W ₂, W ₃ – веса (распределенные нагрузки).

Первое решение задачи о неразрезных балках было опубликовано французским инженером Б.Клапейроном в 1857 году. Он доказал т.н. теорему о трех моментах. Уравнение трех моментов представляет собой соотношение между изгибающими моментами в трех последовательных опорах одной неразрезной балки. Например, в случае неразрезной балки с равномерной нагрузкой на каждом пролете это уравнение имеет вид

M_AL ₁ + 2 M_B (L ₁ + L ₂) + M_CL ₂ = – (W ₁ L ₁³)/4 – (W ₂ L ₂³)/4,

где - M_A, M_B и M_C – изгибающие моменты в трех опорах, L ₁ и L ₂ – длины левого и правого пролетов, W ₁ – нагрузка на левый пролет, а W ₂ – нагрузка на правый пролет.

Нужно написать такое уравнение для каждой пары смежных пролетов, а затем решить полученную систему уравнений. Если число пролетов равно n, то число уравнений будет равно n – 1.

В 1930 году Х.Кросс опубликовал свой метод расчета широкого круга статически неопределимых рам и неразрезных балок. Его «метод распределения моментов» позволяет обходиться без решения систем уравнений, сводя все вычисления к сложению и вычитанию чисел.