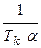Определение периодических режимов при несимметричных колебаниях

Рассмотрим нелинейную систему

Связь между координатами на входе и выходе линейной части

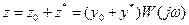(4.7.12)

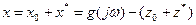(4.7.13)

Учитывая выражение (4.7.3) гармонической линеаризации нелинейного элемента и исключая промежуточные переменные, получим гармонически линеаризованное уравнение системы при несимметричных режимах

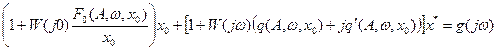; (4.7.14)

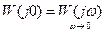– коэффициент передачи линейной части,

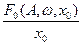– статический коэффициент передачи нелинейного элемента,

Предположим, что на заданном интервале времени А, ω и x ₀ остаются постоянными, при этом уравнение (4.7.14) разбивается на два:

уравнение для постоянной составляющей

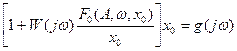, (4.7.15)

уравнение для периодических составляющих

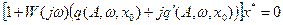. (4.7.16)

Система уравнений (4.7.15, 4.7.16) может быть решена алгебраическим путем. Для этого во втором уравнении системы выделяется действительная и мнимая части, их почленно приравнивают к нулю.

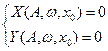
(4.7.17)

В итоге получаем систему из трёх уравнений (4.7.16), (4.7.17) и три неизвестных: А, ω, x ₀. Эта система совместная,следовательно, могут быть найдены переменные А, ω, x ₀.

(4.7.18) (4.7.19)

Автоколебания могут быть найдены и частотными методом. Если известно x₀, то характеристическое уравнение замкнутой системы представляется в виде

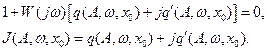
Затем графически решается уравнение

.

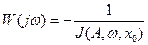Строится годограф АФХ линейной части и обратный годограф АФХ Н.Э. Откуда находятся A и w автоколебаний.

В качестве примера рассмотрим методику исследования несимметричных периодических режимов при постоянном входном воздействии.

Предположим, что g (jω)= g ₀ – постоянная величина, и рассмотрим методику определения несимметричных автоколебательных режимов частотным методом.

Рассмотрим более простой случай, когда нелинейность имеет вид у = F (x), при этом коэффициенты гармонической линеаризации зависят от амплитуды А, смещения x ₀ на выходе Н.Э. и имеют вид q (А,х₀), q' (А,х₀) и F ₀(А, x ₀).

1. Записываются уравнения для постоянных составляющих

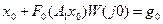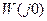; - статический коэффициент передачи линейной части, при w=0.

2. 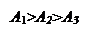Строится прямая линия

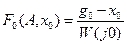
3.

Рис. 4.7.7

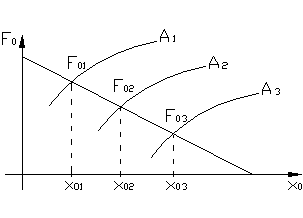
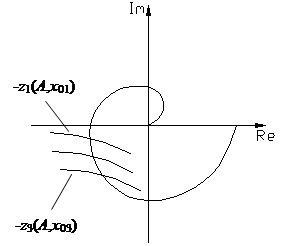
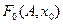По известным выражениям (4.7.6) гармонической линеаризации для ряда фиксированных значений амплитуды и переменной 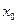строится (рис.4.7.7) семей-ство характеристик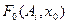
.

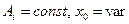4. Строим годограф АФХ W(jω) линейной части.

Затем для ряда дискретных значений х ₀ и переменной А строим семейство обратных АФХ Н.Э.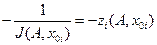
и определяем устойчивость автоколебаний.

В соответствии с критерием –автоколебания устойчивы.

Х 01 <X 02 <X 03

Рис. 4.7.8

Рис. 66

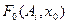5. По точкам пересечения кривых с прямой 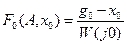строим (рис.4.7.9) график A (х ₀).

6. По точкам пересечения годографа АФХ линейной части с обратной АФХ нелинейного элемента строим (рис.4.7.9) кривую х ₀(А).

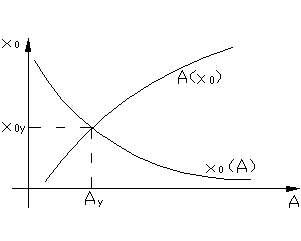
Рис. 4.7.9

Рис. 4.7.9

7. Графическое решение уравнений А(х₀) и х₀(А) даёт искомые параметры устойчивых автоколебаний: Х_0у и А_0у.

e

e

Глава 5. Преобразование структурных схем нелинейных САУ

Для исследования устойчивости автоколебательных режимов многоконтурные нелинейные системы с помощью структурных преобразований необходимо приводить к одноконтурным, одного из следующих видов:

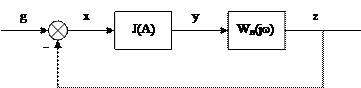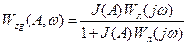. (5.1 а)

		Рис. 5.1 а
		Рис. 5.1 б
		Рис. 5.1 в

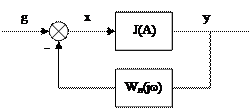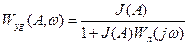.(5.1 б)

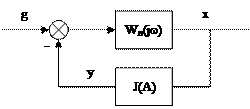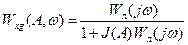.(5.1 в)

Все структуры позволяют найти характеристическое уравнение:

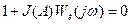, (5.1.д)

поэтому определение параметров и устойчивости автоколебаний можно проводить по любой из выше представленных структур.

Из этого рассмотрения видно, что первым этапом анализа устойчивости нелинейных САУ является выполнение структурных преобразований, а вторым этапом составление уравнения (5.1.д).

Структурные преобразования нелинейных систем можно производить линейным и нелинейным способом. Преобразования в нелинейных системах отличаются от преобразований в линейных САУ, т.к. амплитуда сигнала на входе НЭ должна оставаться неизменной независимо от выполняемых преобразований, поэтому линейные звенья нельзя переносить через нелинейный элемент. Линейные преобразования выполняются по известным правилам и являются эквивалентными, т.е. передаточная функция замкнутой системы до преобразования равна передаточной функции замкнутой системы после преобразования. После нелинейных преобразований с исходным совпадает только характеристическое уравнение (5.1.д).

Рассмотрим несколько примеров с линейными и нелинейными преобразованиями структурных схем.

Пример 1. Нелинейность в прямом пути внутреннего контура.

		Рис. 5.2

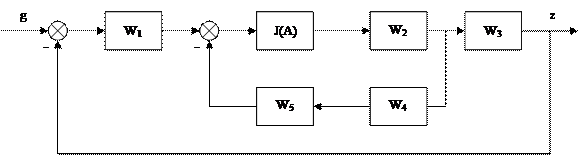Запишем по формуле Мэзона ПФ замкнутой гармонически линеаризованной нелинейной САУ 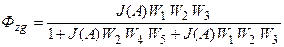. (5.2)

Проведём линейные преобразования структурной схемы

	Рис. 5.3

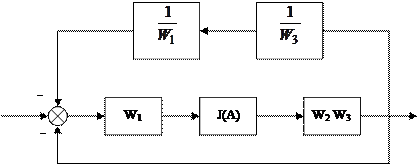Просуммируем обратные связи. Ввести переменные g, z

		Рис. 5.4

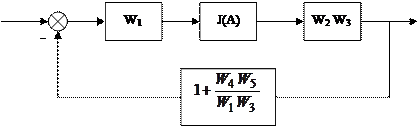В окончательном виде:

Ввести переменные g, z

		Рис. 5.5

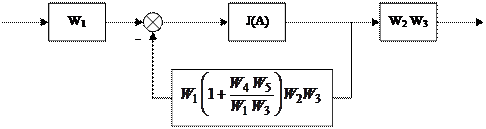Для проверки запишем ПФ замкнутой нелинейной САУ

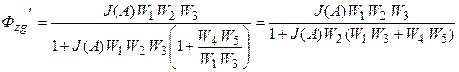(5.3)

Из совпадения выражений (5.3) и (5.2) делаем вывод, что преобразования выполнены верно.

Пример2. Преобразование структурной схемы нелинейным способом

Нелинейные преобразования основаны на отключении одной из линий связи и вынесении нелинейностей из внутреннего контура. Такие преобразования не являются эквивалентными. Они позволяют получить то же самое характеристическое уравнение, но не передаточную функцию замкнутой системы.

Разрываем схему и выносим нелинейность из внутреннего контура.

		Рис. 5.6

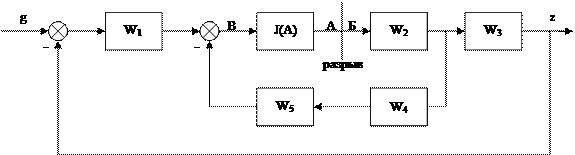Характеристический полином замкнутой системы

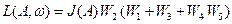, (5.4)

совпадает по виду со знаменателем исходной передаточной функции (5.2), но числитель ПФ будет отличаться от числителя (5.2.). Следовательно, преобразованная структурная схема не позволяет построить эквивалентные переходные процессы.

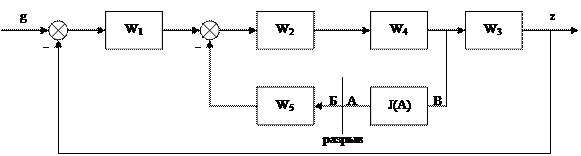
Пример 2. Нелинейность в цепи местной обратной связи

		Рис. 5.7

Разомкнём линию связи за нелинейностью и извлечём НЭ из внутреннего контура

		Рис. 5.8

		Рис. 5.9

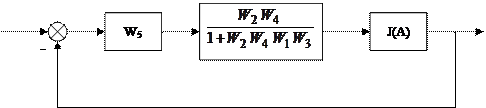Место разрыва устранено соединением точек А и Б линией связи.

Найдём характеристическое уравнение структуры (рис. 5.9)

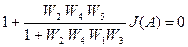(5.5)

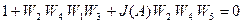(5.6)

По исходной структурной схеме (рис.5.7) получим ПФ замкнутой системы

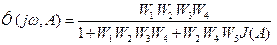. (5.7)

Как видно, знаменатель выражения (5.7) является совпадает с характеристическим уравнением (5.6).

Если в структурных схемах встречаются две нелинейности, расположенные рядом (рис.5.10), то они объединяются в одну эквивалентную нелинейную характеристику (рис.5.11). Затем преобразование структурных схем проводят веше рассмотренными способами.

		Рис. 5.10
		Рис. 5.11

e

e

Глава 6. Нелинейные системы с коррекцией.

6.1. Выбор корректирующих устройств, препятствующих

e

e

возникновению автоколебаний в нелинейных системах

В нелинейных системах коррекция может быть и линейной, и нелинейной. Автоколебания могут быть как естественно присутствующими, так и специально вводимые.

Линейные и нелинейные КУ вводятся со следующими целями:

а) устранение пересечения годографов линейной части и нелинейного элемента на комплексной плоскости, для исключения автоколебаний;

б) с целью обеспечения требуемой амплитуды и частоты автоколебаний, т.е. обеспечение пересечения годографов в нужной точке.

С помощью линейных корректирующих устройств деформируется годограф W(jw), а с помощью нелинейных z(A), и те и другие КУ могут быть последовательными или встречно-параллельными (в виде обратной связи).

Местные обратные связи имеют меньше ограничений на место включения и уменьшают зависимость показателей качества системы от изменения параметров охваченной части.

e

e

6.1.1. Выбор линейных последовательных корректирующих устройств

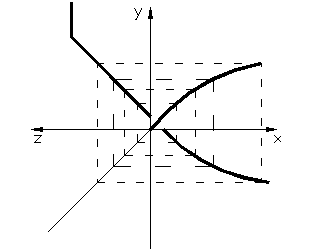
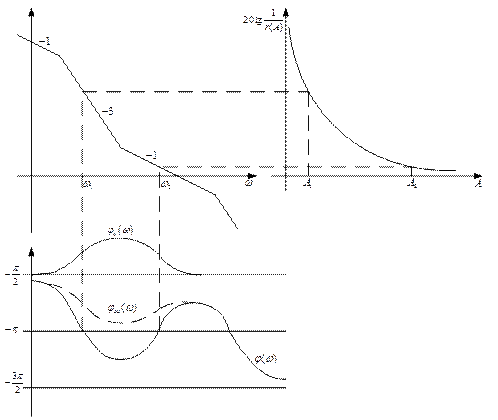
Рассмотрим систему с однозначной нелинейностью. Условие баланса фаз и амплитуд
выполняется на частотах ω₁ и ω₂

Рис. 6.1.1.1

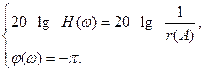
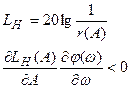(6.1.1.1)

Для устранения автоколебаний необходимо введение корректирующих звеньев фазоопережающего типа.

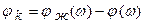(6.1.1.2)

Рис. 6.1.1.2

		Рис. 6.1.1.3

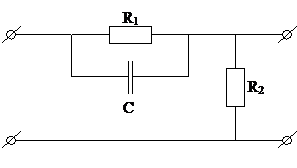
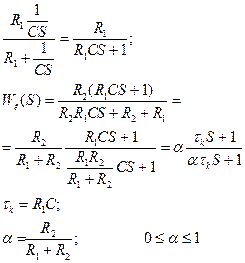
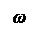В случае с неоднозначными нелинейными характеристиками задача синтеза существенно усложняется. Нет общей методики синтеза линейных КУ.

Общие рекомендации сводятся к следующему:

Wж(jw)

w

W(jw)

Нужно построить годограф обратной АФХ нелинейного элемента. Определяется область частот, в которой необходимо скорректировать систему: ω _а ω _б. Годограф АФХ линейной части корректируется таким образом, чтобы исключить автоколебания (чтобы не было пересечений).

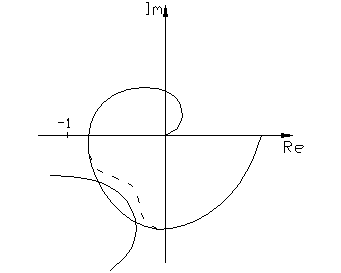
В точке б – устойчивые автоколебания

	а

б

После определения ориентировочной области для корректирующих устройств переходят к ЛАХ и рассчитывают вид и параметры КУ.

Нет стрелок А

6.1.2.

e

e

Выбор встречно-параллельных корректирующих устройств

(местных обратных связей)

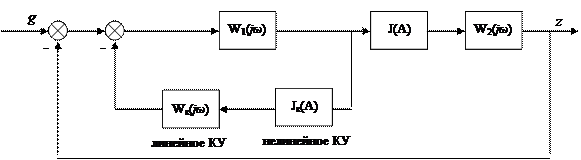
Рассмотрим рекомендации по выбору местных обратных связей линейного или нелинейного вида.

		Рис. 6.1.2.1

J (A) – основная нелинейность (однозначная)

J _к(A) – ПФ корректирующей нелинейности

W _к(jω) – ПФ линейного КУ

Характеристическое уравнение:

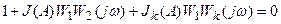(6.1.2.1)

Для выбора корректирующих устройств: нелинейного J _к(A) и линейного W _к(jω) воспользуемся дополнительными условиями.

1 Условие. Примем 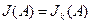, т.е. корректирующая нелинейность и основная – одинаковы.

Из уравнения (6.1.2.1) получим:

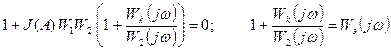. (6.1.2.2)

Условие баланса фаз и амплитуд:

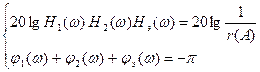(6.1.2.3)

Выбором 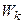добиваются устранения автоколебаний, т.е. чтобы суммарная ФЧХ не пересекала линии -p в области где выполняется условие

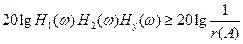
2 Условие. Примем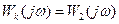

Тогда характеристическое уравнение имеет вид:

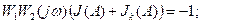(6.1.2.4)

Если объединить обе нелинейные характеристики в одну, получим: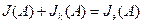

Условие баланса фаз и амплитуд:

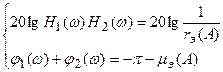(6.1.2.5)

В данном случае устранения автоколебаний добиваются выбором 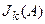в эквивалентной нелинейности.

3 Условие. Корректирующую нелинейность 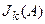представим в виде:

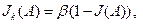(6.1.2.6)
где β- коэффициент, .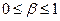

Тогда уравнение (6.1.2.4) можно привести к виду:

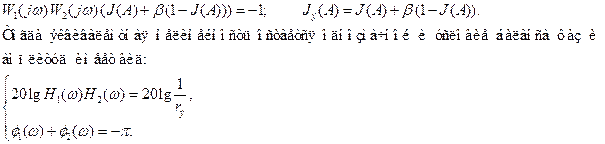
В этом случае для устранения автоколебаний необходимо выбирать β таким образом, чтобы ФЧХ 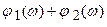не пересекала линию 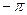в заданном диапазоне амплитуд А.

4 Случай. Представим корректирующую нелинейность в форме (6.1.2.6) и подставим в уравнение (6.1.2.1)

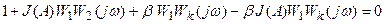
Выделим линейную часть и нелинейный элемент.

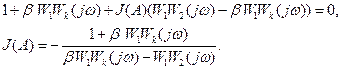(6.1.2.6)

Устранения автоколебаний добиваются выбором линейного КУ 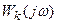и коэффициента b в диапазоне от 0 до 1.

e

e

6.2. Системы с переменной структурой (СПС)

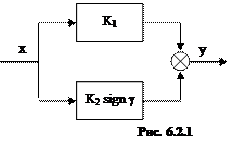
Характерной особенностью СПС является наличие в них ключевого элемента, скачкообразно изменяющего один из параметров системы.

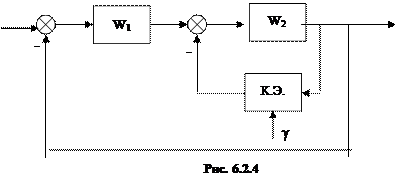
Наибольшее распространение имеет статический ключевой элемент (рис.6.2.1, 6.2.2).

		Рис. 6.2.2

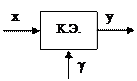g - управляющий сигнал

1. Ключевой элемент имеет два параллельных канала и описывается выражениями:

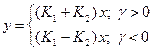(6.2.1)

Обычно в СПС используется два частных случая КЭ:

а) инвертирующий КЭ при К₁=0, К₂=0.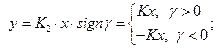

предназначается для инвертирования сигнала х при .,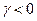

б) размыкающий ключевой элемент при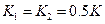

.

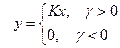Такой КЭ разрывает цепь передачи сигнала х при .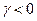

При К₂=0 и К₁ =К, КЭ превращается в линейное звено у=Кх.

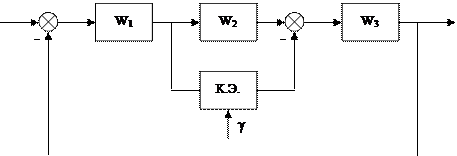
Ключевой элемент может быть включен в прямую цепь (последовательно) рис.6.2.3, параллельную цепь (рис.6.2.5) или в цепь ОС (рис.6.2.4). Он может быть естественно присутствующим или специально вводимым для улучшения динамических свойств системы..

		Рис. 6.2.3
		Рис. 6.2.5
		Рис. 89

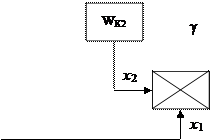
Сигнал управления g обычно формируют в виде произведения: 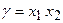, где х ₁ и х ₂ – либо естественно присутствующие, либо специально вводимые сигналы. Широкое применение этого закона обусловлено относительной простотой реализации КЭ, в котором анализ знаков х ₁ и х ₂ выполняется с помощью логических устройств.

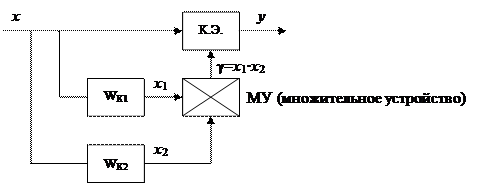
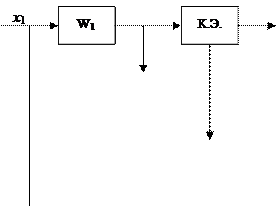
Структурная схема последовательного ключевого корректирующего устройства (ККУ) представлена на рис. 6.2.6.

		Рис. 6.2.6

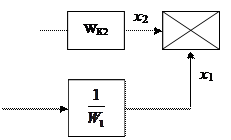
Звенья с ПФ W_К1 и W_К2 формируют сигналы х₁ и х_2. Для того чтобы ККУ вносило в систему положительные фазовые сдвиги передаточные функции W _К1, W _К2 должны быть дифференциального типа. Дифференцирующие звенья существенно увеличивают уровень помех. Более рациональным является использование, вместо сигналов х₁ и х₂, сигналов, естественно присутствующих в системе. Так, например, если КЭ включается на выходе инерционного звена с ПФ 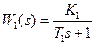, то целесообразно применять схему включения ККУ (рис.6.2.7а). После эквивалентных преобразований структурной схемы из рис.(6.2.7б) видно, что сигнал 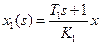. В этом случае исключается дифференцирующее звено W _К1, а его роль выполняет инерционное звено W ₁ системы.

g

		Рис. 6.2.7 а		Рис. 6.2.7 б

Если линейная часть системы обладает фильтрующими свойствами, то для анализа СПС удобно применять метод гармонической линеаризации, а СПС не выше второго порядка обычно анализируют методом фазовой плоскости.