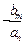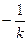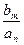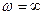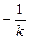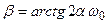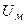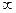В общем случае для всякой системы дифференциальных уравнений относительно нетрудно подобрать определенно положительную функцию V(x1,,...,xn), которая может служить функцией Ляпунова.Основной проблемой данного метода является то, что не всякая такая функция имеет знакоопределенную или знакопостоянную производную W.
А.М.Ляпунов рекомендовал сначала выбирать отрицательно определенную функцию 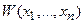 , а затем определять соответствующую положительную функцию
, а затем определять соответствующую положительную функцию 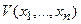 .
.
Для линейных системa функцию 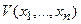 ищут в виде квадратичной формы:
ищут в виде квадратичной формы:
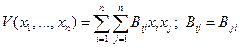 (7.3.1)
(7.3.1)
Для определения коэффициентов Bij задаются функцией 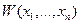 в виде отрицательной квадратичной формы:
в виде отрицательной квадратичной формы:
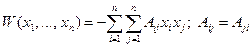 (7.3.2)
(7.3.2)
Предположим, что уравнения, описывающее динамику системы, имеют вид:
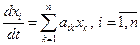 (7.3.3)
(7.3.3)
Тогда из выражения (7.31) с учетом (7.3.3) получим выражение для производной:
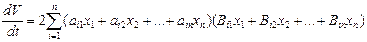 (7.3.4)
(7.3.4)
Приравняв выражения (7.3.4) и (7.3.2), получим:
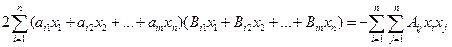
Затем, сгруппировав и приведя подобные члены, можно приравнять коэффициенты в левой и правой части. В итоге получим уравнения для определения коэффициентов Bij:
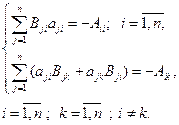 (7.3.5)
(7.3.5)
Полагая величины 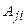 заданными, можно решить систему (7.3.5) относительно коэффициентов
заданными, можно решить систему (7.3.5) относительно коэффициентов 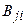 и, получив в результате функцию
и, получив в результате функцию 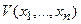 , производная которой
, производная которой 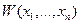 имеет заданный вид.
имеет заданный вид.
Коэффициенты 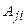 при этом назначаются так, чтобы функция
при этом назначаются так, чтобы функция 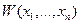 была заведомо знакоопределенной. Это можно сделать разными способами, например, принять
была заведомо знакоопределенной. Это можно сделать разными способами, например, принять 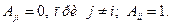
Тогда производная 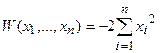 имеет определённо отрицательный вид.
имеет определённо отрицательный вид.
В этом случае коэффициенты 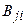 определяются из системы уравнений:
определяются из системы уравнений:
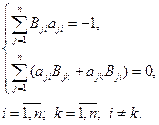 (7.3.6)
(7.3.6)
Пример:
выбор функции Ляпунова для линейной системы второго порядка (n=2).
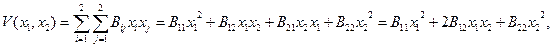 (7.3.7)
(7.3.7)
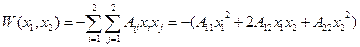 (7.3.8)
(7.3.8)
Примем 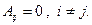
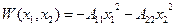 .
.
Предположим, что уравнения возмущённого движения системы имеют вид:
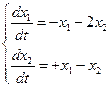 (7.3.9)
(7.3.9)
Откуда найдём значения коэффициентов
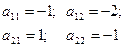 (7.3.10)
(7.3.10)
Используя формулы соответствия:
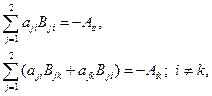 (7.3.11)
(7.3.11)
получим
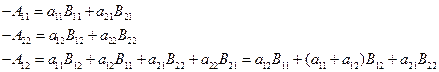 (7.3.12)
(7.3.12)
Учитывая значения коэффициентов (7.3.10):
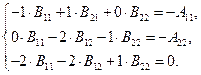 (7.3.13)
(7.3.13)
Примем
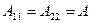 (7.3.15)
(7.3.15)
и решим систему уравнений
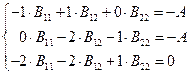
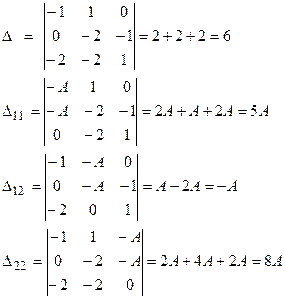 (7.3.16)
(7.3.16)
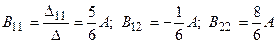 (7.3.17)
(7.3.17)
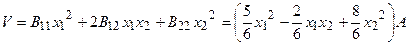 (7.3.18)
(7.3.18)
При 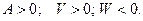
В случае нелинейных систем единая методика выбора функции Ляпунова отсутствует, однако для систем отдельных типов имеются рекомендации по выбору функции Ляпунова. Например, для системы вида:
 | |||
|
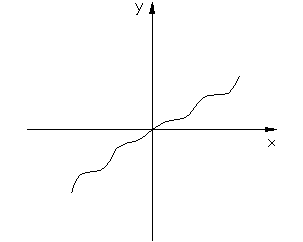
с характеристикой (рис.7.3.2) НЭ, удовлетворяющей условиям
f (0)=0, 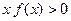
А.И. Лурье и В.М. Постниковым был предложен следующий подход: функция Ляпунова находится как квадратичная форма от координат системы плюс интеграл от нелинейности
|
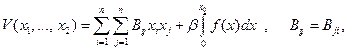 β – постоянные коэффициенты (7.3.19)
β – постоянные коэффициенты (7.3.19)
Можно показать, что поверхности постоянных значений V=const, взятых в такой форме, содержат внутри себя начало координат и имеют значения d, возрастающие по модулю по мере удаления от начала координат. Эти поверхности заполняют все фазовое пространство и при соответствующем выборе значений 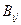 и
и 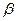 могут служить для определения устойчивости равновесия системы в целом (и в «малом», и в «большом»).
могут служить для определения устойчивости равновесия системы в целом (и в «малом», и в «большом»).
Пример: проверить устойчивость равновесия в системе

Линейная часть описывается выражением
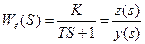 . (7.3.20)
. (7.3.20)
|
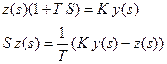
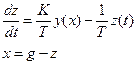
При определении устойчивости положения равновесия внешние воздействия должны отсутствовать, следовательно входной сигнал g =0, поэтому  .
.
Дифференциальное уравнение нелинейной системы
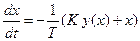 . (7.3.25)
. (7.3.25)
Функцию Ляпунова V выбираем в виде квадратичной формы плюс интеграл от нелинейности 
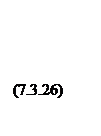
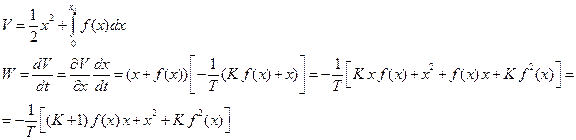 Если нелинейная характеристика проходит через первый и третий квадранты, то
Если нелинейная характеристика проходит через первый и третий квадранты, то 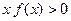 . При определённо положительной функции Ляпунова
. При определённо положительной функции Ляпунова 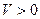 из (7.3.26) следует, что
из (7.3.26) следует, что 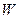 – функция определенно отрицательная при
– функция определенно отрицательная при 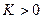 , что и является условием устойчивости.
, что и является условием устойчивости.
7.4. Частотный критерий абсолютной устойчивости
(критерий В.М. Попова)
Румынский учёный В.М.По'пов предложил частотный метод определения абсолютной устойчивости положения равновесия нелинейных систем. Рассматривается устойчивость собственного движения нелинейной системы, состоящей из двух звеньев.
 | |||
|
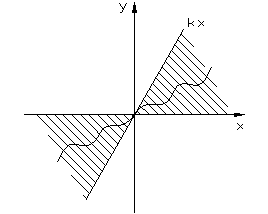
На нелинейность накладываются следующие ограничения:
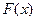 - однозначная нелинейная функция любой формы, принадлежащая сектору (0,k) и проходящая через начало координат.
- однозначная нелинейная функция любой формы, принадлежащая сектору (0,k) и проходящая через начало координат.
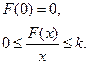
|
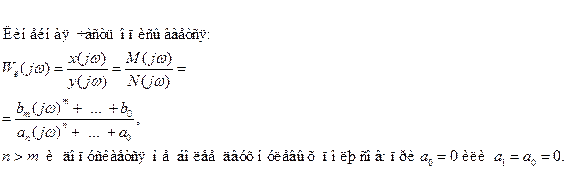
Остальные полюса должны лежать в левой полуплоскости.
Теорема В.М.Попова: для установления абсолютной устойчивости положения равновесия нелинейной системы достаточно подобрать такое действительное число h >0, чтобы при всех 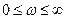 выполнялось условие:
выполнялось условие:
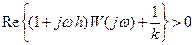 (7.4.1)
(7.4.1)
где k – коэффициент, ограничивающий сектор, внутри которого должна лежать нелинейность.
При наличии одного нулевого полюса требуется выполнение условия: 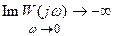 .
.
При наличии двух нулевых полюсов требуется выполнение условия: 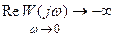 .
.
Графическая интерпретация уравнения 7.4.1.
Для удобства графической интерпретации введем модифицированные частотные характеристики линейной части.
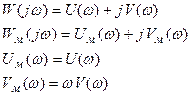 (7.4.2)
(7.4.2)
Модифицированная АФХ WM(jω) имеет особенности, отличающие её от W(jω). Если разность степеней 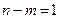 , то годограф
, то годограф 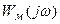 заканчивается на мнимой оси (рис.7.4.3). Если
заканчивается на мнимой оси (рис.7.4.3). Если 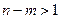 , то WM(jω) и W(jω) совпадают при ω=0, ω=1 и ω=∞.
, то WM(jω) и W(jω) совпадают при ω=0, ω=1 и ω=∞.
|
|
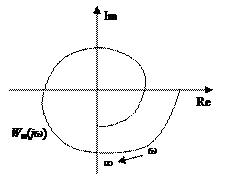
Рис.7.4.3
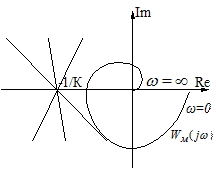
|
|
|
|

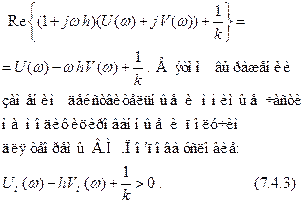
Рис. 7.4.4
|
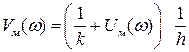 , (7.4.4)
, (7.4.4)
то получим уравнение (7.4.4) прямой линии на комплексной плоскости 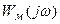 , проходящей через точку
, проходящей через точку 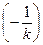 .
.
Отсюда вытекает графическая интерпретация теоремы В.М.Попова: для установления абсолютной устойчивости нелинейной системы достаточно на плоскости 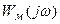 подобрать такую прямую, проходящую через точку
подобрать такую прямую, проходящую через точку 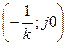 , чтобы годограф модифицированной АФХ
, чтобы годограф модифицированной АФХ 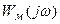 лежал справа от этой прямой (рис.7.4.4).
лежал справа от этой прямой (рис.7.4.4).
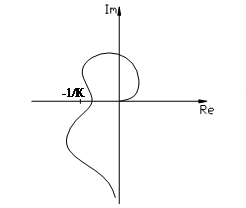
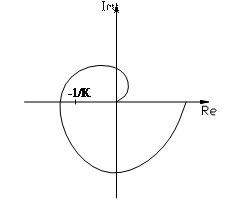
На рис. 7.4.5 показаны случаи невыполнения теоремы.
 | |||||||||
 | |||||||||
| |||||||||
| |||||||||
| |||||||||
|
|
Нелинейная система второго порядка имеет передаточную функцию линейной части вида:
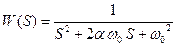 (7.4.4)
(7.4.4)
ω0 – величина, обратная постоянной времени.
Необходимо определить, при каких значениях k система будет абсолютно устойчива, если характеристика нелинейного элемента лежит в секторе (0, k).
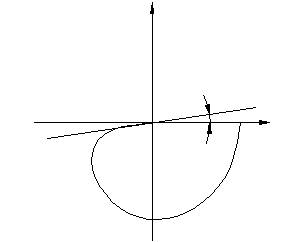
Модифицированная АФХ имеет вид:
|
|
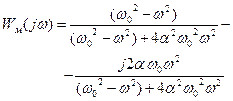
|
|

|
|
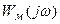 лежит в нижней плоскости и при
лежит в нижней плоскости и при 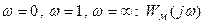 совпадает с
совпадает с 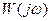
Из анализа графика АФХ можно сделать вывод, что система абсолютно устойчива при любых значениях k, вплоть до k = ∞, т.к. в начале координат (ω=∞) кривая лежит правее касательной с углом β к вещественной оси. Поэтому всегда можно провести прямую Попова через точку -1/К под некоторым углом β. Таким образом, система абсолютно устойчива при всех К, если однозначная нелинейная характеристика принадлежит сектору (0, ∞). Т.е. нелинейная характеристика должна лежать в первом и третьем квадрантах и может иметь при этом любую форму.
Обобщение критерия Попова на случай неустойчивости линейной части.
Если линейная часть системы неустойчива, то нелинейная характеристика не может принадлежать сектору (0,k), т.к. при k=0, что соответствует разомкнутой системе, получается заведомо неустойчивая система, т.к. неустойчива линейная часть. Неустойчивость сохраняется и в области малых значений k. Для применения критерия Попова к САУ с неустойчивой линейной частью, структурную схему системы преобразуют путем охвата линейной части отрицательной жесткой обратной связью с коэффициентом r, а нелинейного элемента параллельной отрицательной связью с коэффициентом r.
 | |||
|
 | |||
 |
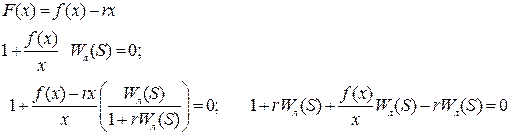 (7.4.5)
(7.4.5)
Коэффициент r выбирают таким образом, чтобы контур с неустойчивой передаточной функцией W (S) стал устойчив, т.е. чтобы передаточная функция преобразованной линейной части 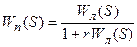 была устойчива.
была устойчива.
Устойчивость 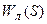 определяется по критерию Найквиста.
определяется по критерию Найквиста.
Условие устойчивости В.М. Попова в этом случае:
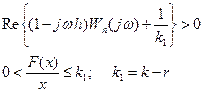 (7.4.6)
(7.4.6)
7.5. Сравнение методов анализа устойчивости нелинейных систем
Рассмотрим область устойчивости (рис.7.5.1) на плоскости обобщённых параметров α, β нелинейной системы. Из рассмотренных методов анализа устойчивости нелинейных систем только с помощью метода фазового пространства можно найти точную границу устойчивости. Этот метод позволяет найти как необходимое, так и достаточное условие устойчивости.
Прямой метод Ляпунова и частотный критерий абсолютной устойчивости В.М. Попова позволяют найти только достаточное, но не необходимое условие устойчивости. При этом области устойчивости (1 и 2) получаются меньше, чем действительная граница, но эти методы гарантируют устойчивость этих в областях (1 и 2). В общем случае метод Ляпунова дает более узкую область достаточных условий, чем метод В.М. Попова. Метод гармонической линеаризации в зависимости от степени выполнения условия фильтра дает приближенное значение области устойчивости, однако, он не гарантирует устойчивость в данной области. Т.е. построенная с помощью метода гармонической линеаризации область устойчивости (3) может быть шире, чем в действительности.

Нанести параметры α, β
1 – граница по методу В.М. Попова
2 – граница по методу Ляпунова
|
Д.Г.У. – действительная граница
устойчивости
|
Глава 8. Исследование устойчивости переходных процессов в
нелинейных системах.
8.1. Абсолютная устойчивость процессов в нелинейной системе
 | |||||
 | |||||
|
Выполнение в нелинейной системе (рис.8.1.1) только условий абсолютной устойчивости положений равновесия может не обеспечивать абсолютной устойчивости процессов, вызванных каким-либо ограниченным по модулю воздействием g (t).
Б.Н. Наумовым и Я.З. Цыпкиным был предложен критерий абсолютной устойчивости процесса в системе с однозначной нелинейностью.
Основные положения:
Для абсолютной устойчивости процессов в системе с одной однозначной нелинейностью достаточно: 1.Чтобы при заданном 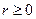 преобразованная передаточная функция линейной части
преобразованная передаточная функция линейной части 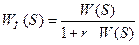 была устойчива, частотная характеристика W(jω) при всех
была устойчива, частотная характеристика W(jω) при всех 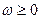 удовлетворяла бы условию
удовлетворяла бы условию 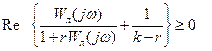 . (8.1.1)
. (8.1.1)
2. Нелинейная однозначная характеристика должна отвечать условию:
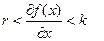 (8.1.2)
(8.1.2)
Т.е. производная нелинейной характеристики (крутизна 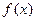 ) должна лежать в секторе (r, k).
) должна лежать в секторе (r, k).

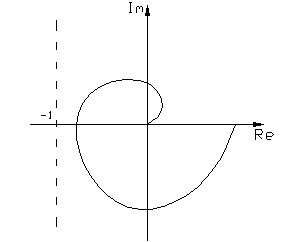 В случае устойчивой линейной части r=0, тогда условие
В случае устойчивой линейной части r=0, тогда условие 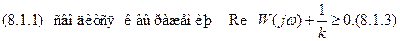 или к виду
или к виду 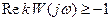 (8.1.4)
(8.1.4)
Из условия (8.1.4) следует, что процессы будут абсолютно устойчивы, если АФХ 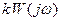 расположена правее прямой
расположена правее прямой 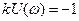
 | |||||
| |||||
| |||||
|
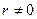 . Введем в рассмотрение параметр
. Введем в рассмотрение параметр 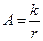 . С учетом этого выражение (8.1.1) запишем в виде:
. С учетом этого выражение (8.1.1) запишем в виде: 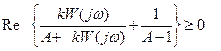 (8.1.5)
(8.1.5)
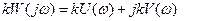 (8.1.6)
(8.1.6)
Найдем на комплексной плоскости 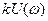 и
и 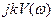 геометрическое место точек, соответствующее постоянным значениям A=const. Для этого заменим в выражении (8.1.5) знак неравенства на знак равенства. Затем, подставляя выражение (8.1.6) в выражение (8.1.5), прибавив и отняв
геометрическое место точек, соответствующее постоянным значениям A=const. Для этого заменим в выражении (8.1.5) знак неравенства на знак равенства. Затем, подставляя выражение (8.1.6) в выражение (8.1.5), прибавив и отняв 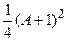 , выделив действительную часть и приравняв ее к нулю, получим:
, выделив действительную часть и приравняв ее к нулю, получим:
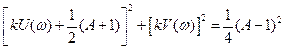 (8.1.7)
(8.1.7)
Выражение (8.1.7) описывает семейство окружностей с радиусом 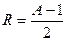 , проходящих через точку с координатами
, проходящих через точку с координатами 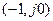 и лежащих левее прямой
и лежащих левее прямой 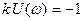 (семейство А -окружностей).
(семейство А -окружностей).
|
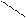
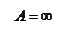
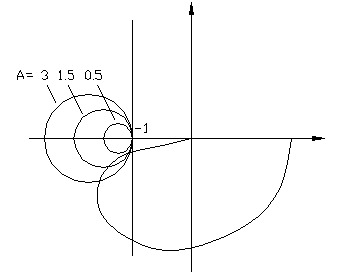 Система обладает абсолютной устойчивостью.
Система обладает абсолютной устойчивостью.
|

|
|
|
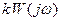 , удовлетворяя критерию Найквиста, не пересекала бы соответствующие A-окружности.
, удовлетворяя критерию Найквиста, не пересекала бы соответствующие A-окружности.
|
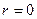
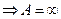 и А-окружность переходит в прямую линию (окружность бесконечного радиуса.
и А-окружность переходит в прямую линию (окружность бесконечного радиуса. 8.2. Исследование абсолютной устойчивости процессов по ЛЧХ
(логарифмический критерий абсолютной устойчивости)
Рассмотрим систему с устойчивой линейной частью и нелинейностью, отвечающей условию 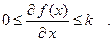 . (8.2.1)
. (8.2.1)
Условие абсолютной устойчивости имеет вид:
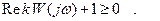 (8.2.2)
(8.2.2)
Частотные характеристики линейной части представим в виде:
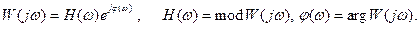 (8.3.3)
(8.3.3)
Условие (8.2.2) с учетом (8.3.3) можно заменить равноценным условием
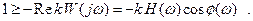 (8.2.4)
(8.2.4)
Условие (8.2.4) автоматически выполняется в диапазоне частот, где 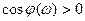 , поэтому необходимо исследовать систему лишь при значениях
, поэтому необходимо исследовать систему лишь при значениях 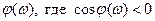
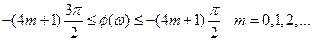 (8.2.5)
(8.2.5)
Следовательно вместо условия (8.2.4) можно потребовать выполнения равносильного ему условия:
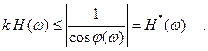 (8.2.6)
(8.2.6)
Если перейти к логарифмическим характеристикам, получим:
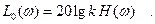 (8.2.7)
(8.2.7)
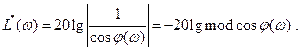 (8.2.8)
(8.2.8)
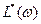 –логарифмическая характеристика критического коэффициента передачи H*(ω).
–логарифмическая характеристика критического коэффициента передачи H*(ω).
Формулировка критерия: При ограниченном возмущении g (t) и нелинейной характеристике, удовлетворяющей условию (8.2.1), для абсолютной устойчивости процессов в системе достаточно, если в диапазоне частот, где выполняется условие (8.2.5), нормированная ЛАХ 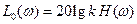 не пересекает ЛАХ критического коэффициента передачи
не пересекает ЛАХ критического коэффициента передачи 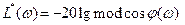 , т.е. условие устойчивости кратко можно представить:
, т.е. условие устойчивости кратко можно представить:
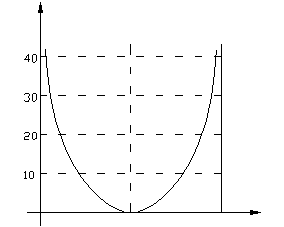
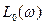
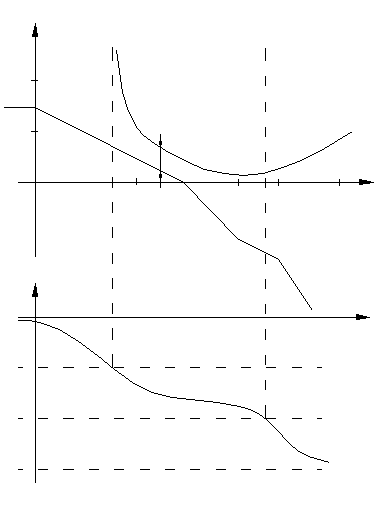
При практическом использовании ЛАХ 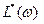 обычно строят (рис. 8.2.1) в диапазоне углов:
обычно строят (рис. 8.2.1) в диапазоне углов: 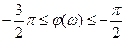 по формуле (8.2.8).
по формуле (8.2.8).
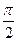 и больших
и больших 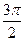 условие (8.2.4) выполняется автоматически и проверки не требует..
условие (8.2.4) выполняется автоматически и проверки не требует..
|
|
| ||||||
| ||||||||
|
 - функция чётная, то знак
- функция чётная, то знак 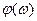 значения не имеет. Следует отметить, что на концах интервала рассмотрения
значения не имеет. Следует отметить, что на концах интервала рассмотрения 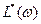 стремится к бесконечности.
стремится к бесконечности.
|
|
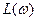 и
и 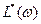 можно определить величину смещения b,, обеспечивающую абсолютную устойчивость процесса.
можно определить величину смещения b,, обеспечивающую абсолютную устойчивость процесса. Если обозначить через Kпред коэффициент передачи приведенной линейной части в точке касания 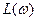 и
и 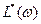 , то
, то 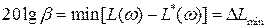 .
.
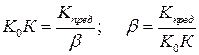 (8.2.10)
(8.2.10) Пример
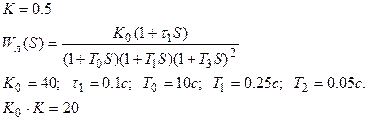 (8.2.11)
(8.2.11)
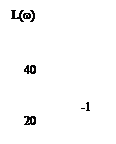 | |||||||||||||||
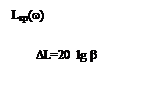 | |||||||||||||||
|  | ||||||||||||||
 | |||||||||||||||
| |||||||||||||||
 |
| |||||||||
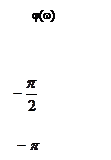 | |||||||||
| |||||||||
| |||||||||
| |||||||||
Условие устойчивости выполняется. K0 можно еще увеличить на 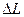 , чтобы увеличить быстродействие и точность.
, чтобы увеличить быстродействие и точность.
 2015-07-04
2015-07-04 1022
1022