Теорема. Пусть комплекс условий S воспроизводится n раз, причём каждый раз событие A может наступить с одной и той же вероятностью p (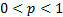 ) независимо от результатов предыдущих опытов. Тогда вероятность того, что событие A произойдёт ровно k раз в n испытаниях, определяется по формуле Бернулли
) независимо от результатов предыдущих опытов. Тогда вероятность того, что событие A произойдёт ровно k раз в n испытаниях, определяется по формуле Бернулли
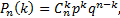 (2.1)
(2.1)
где 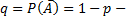 вероятность непоявления в одном испытании.
вероятность непоявления в одном испытании.
Доказательство. Пусть 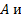
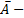 соответственно появление и непоявление события A в единичном испытании,
соответственно появление и непоявление события A в единичном испытании, 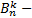 событие, состоящее в том, что в n независимых испытаниях событие A появилось ровно k раз. Тогда
событие, состоящее в том, что в n независимых испытаниях событие A появилось ровно k раз. Тогда
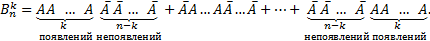
Всего получим 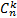 слагаемых (
слагаемых (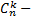 сколькими способами можно расположить
сколькими способами можно расположить 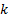 объектов по
объектов по 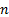 местам без учета порядка). Тогда
местам без учета порядка). Тогда
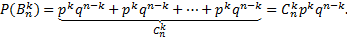
Чтобы нагляднее представить свойства ряда вероятностей 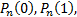 …,
…, 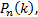 …,
…, 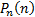 , в прямоугольной системе координат отмечают точки с координатами
, в прямоугольной системе координат отмечают точки с координатами 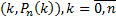 и соединяют их ломаной (рисунок 2.1).
и соединяют их ломаной (рисунок 2.1).
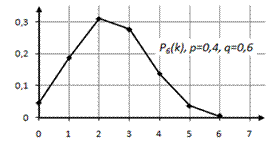
Рисунок 2.1
Число наступлений события называется наивероятнейшим, если вероятность наступления события данное число раз в этой серии испытаний наибольшая по сравнению с вероятностями других исходов. На рисунке 2.3 наивероятнейшее число 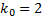 .
.
Пусть n – число независимых испытаний, p – вероятность наступления события в отдельном испытании. Тогда наивероятнейшее число наступлений события 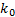 удовлетворяет неравенству
удовлетворяет неравенству
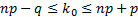 , (2.2)
, (2.2)
где 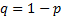 .
.
Так как разность 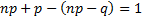 , то всегда найдётся целое число
, то всегда найдётся целое число 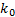 , удовлетворяющее написанному выше двойному неравенству. При этом, если
, удовлетворяющее написанному выше двойному неравенству. При этом, если 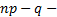 целое число, то наивероятнейших чисел два:
целое число, то наивероятнейших чисел два: 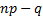 и
и 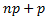 .
.
Пример 2.1. Вероятность изготовления на автоматическом станке стандартной детали равна 0,8. Найти наивероятнейшее число появления бракованных деталей из 5 отобранных и вероятность этого числа.
Решение. Вероятность изготовления бракованной детали 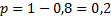 . По формуле (2.2):
. По формуле (2.2): 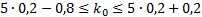 или
или 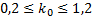 .
.
Единственное целое число, удовлетворяющее этому неравенству, 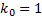 , его вероятность находим по формуле Бернулли
, его вероятность находим по формуле Бернулли
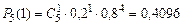 .
.
Пример 2.2. Сколько раз надо подбросить игральную кость, чтобы наивероятнейшее число выпадений двойки было равно 32?
Решение. В данном случае 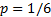 ,
, 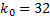 . Требуется найти число независимых испытаний n. Величины
. Требуется найти число независимых испытаний n. Величины 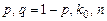 связаны между собой соотношением (2.2):
связаны между собой соотношением (2.2): 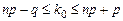 , откуда
, откуда
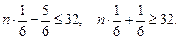
Из первого неравенства 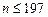 , а из второго
, а из второго 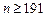 . Таким образом, необходимо провести от 191 до 197 подбрасываний игральной кости.
. Таким образом, необходимо провести от 191 до 197 подбрасываний игральной кости.
 2015-07-04
2015-07-04 4999
4999







