К сожалению, ход ломаной линии нельзя передать простым уравнением, к тому же на нем сказывается способ интервального разбиения оси абсцисс, а также уровень репрезентативности в разных областях распределения. В этом смысле предпочтительнее единственная прямая линия регрессии, подчеркивающая основные тенденции зависимости признаков, которая может быть выражена простым уравнением линии: y = ax + b.
Судить о том, как меняется одна величина по мере изменения другой, позволяет коэффициент регрессии (a), показывающий, на какую величину в среднем изменяется один признак (y) при изменении другого (x) на единицу измерения (точнее, на какую величину один признак отклоняется от своей средней при некотором отклонении другого признака от своей средней):
y − My = a ∙ (x −Mx).
Простые преобразования:
y = a ∙ x + My − a ∙ Mx, b = My − a ∙ Mx
и приводят к уравнению линии: y = ax + b.
 |
Рис. 13. Линейная регрессия
Рассчитать коэффициенты уравнения регрессии позволяет метод наименьших квадратов, основная идея которого состоит в том, чтобы линия регрессии прошла на наименьшем удалении от каждой точки, т. е. чтобы сумма квадратов расстояний от всех точек до прямой линии была наименьшей. В математической статистике показано, что для случая двумерного нормального распределения лучшей (эффективной, несмещенной и пр.) линией, описывающей зависимость одного признака от другого, может быть только линия частных средних арифметических.
Вычисления коэффициентов линейной регрессии y = ax + b ведутся по следующему алгоритму. Сначала найдем вспомогательные величины:
Cx = Σ x ² − (Σ x)² / n,
Cy = Σ y ² − (Σ y)² / n,
Cxy = Σ(x ∙ y) − (Σ x) ∙ (Σ y) / n,
My = Σ y / n, Mx = Σ x / n.
Затем рассчитаем коэффициенты: a = Cxy / Cx, b = My − a ∙ Mx.
Оценить значимость коэффициента регрессии позволяет критерий t Стьюдента, проверяющий нулевую гипотезу Но: а = 0, коэффициент регрессии значимо от нуля не отличается. С этой целью рассчитывается ошибка коэффициента регрессии ma:
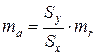 , где mr – ошибка коэффициента корреляции (см. с. 62),
, где mr – ошибка коэффициента корреляции (см. с. 62),
и вычисляется значение критерия:
t = (a − 0) / ma = a / ma ~ t (0.05, n − 2).
Смысл этого критерия состоит в следующем. Коэффициент регрессии a характеризует сопряженность пропорционального изменения двух признаков, т. е. отвечает за то, что линия регрессии имеет некоторый угол относительно оси абсцисс. Значение a = 0 означает, что линия регрессии идет параллельно оси ОХ, что при изменении признака x признак y не меняется, т. е. что y не зависит от x. Значения коэффициента, отличные от нуля, говорят о том, что взаимосвязь признаков имеет место, при a > 0 зависимость положительная, при a < 0 – отрицательная.
Вернемся к примеру с описанием зависимости между живым весом коров и их приплода (стр. 61). Расчеты для построения уравнения регрессии показаны в таблице 16. Сначала вычисляются квадраты вариант и их произведения, а также суммы вариант, квадратов и произведений. Вычисления ведутся по точным рабочим формулам. Проще всего это делать в среде Excel, с помощью команды Сервис \ Анализ данных \ Регрессия.
Таблица 16
| i | у | х | у ² | х ² | х ∙ у | Y | (y − Yi)² | t ∙ mY | min Y | max Y |
| 25.6 | 0.31 | 2.0 | 23.6 | 27.5 | ||||||
| 27.1 | 1.29 | 1.7 | 25.5 | 28.8 | ||||||
| 28.8 | 4.65 | 1.4 | 27.4 | 30.2 | ||||||
| 32.2 | 0.04 | 1.2 | 31.0 | 33.4 | ||||||
| 34.2 | 0.06 | 1.3 | 32.9 | 35.5 | ||||||
| 37.1 | 0.76 | 1.7 | 35.4 | 38.9 | ||||||
| 38.9 | 0.81 | 2.1 | 36.8 | 41.0 | ||||||
| Σ | 7.92 |
Проведем последовательные расчеты вручную. Сначала определим вспомогательные величины:
n = 7,
Cxy = Σ(x∙y) −(Σ x)∙(Σ y)/n = 103144 − 3150 ∙ 224 / 7 = 2344,
Cy = Σ y ² − (Σ y)² / n = 7330 − 224² / 7 = 162,
Cx = Σ x ² − (Σ x)² / n = 1453158 − 3150² / 7 = 35658,
затем – параметры:
My = Σ y / n = 224 / 7 = 32,
Mx = Σ x / n = 3150 / 7 = 450,
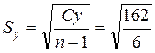 = 5.2,
= 5.2,
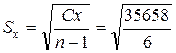 = 77.1,
= 77.1,
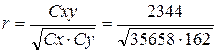 = 0.975,
= 0.975,
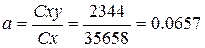 ,
,
b = My − a∙Mx = 32 − 0.0657∙450 = 2.419.
Получено уравнение линейной регрессии Y = 0.0657 x + 2.419, которое позволяет рассчитать теоретические значения Y (табл. 16, графа 7).
Далее найдем ошибку коэффициента регрессии:
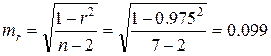 ,
,
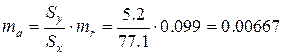 ,
,
и, наконец, критерий t Стьюдента для проверки значимости коэффициента регрессии: ta = a / ma = 0.0657 / 0.00667 = 9.84.
Для уровня значимости α = 0.05 и числа степеней свободы df = n −2=5 находим табличное значение критерия Стьюдента t (0.05,5) = 2.57. Полученная величина (9.84) превышает табличную (2.57), что говорит о статистической значимости коэффициента регрессии (a), о достоверности его отличия от нуля. Масса тела теленка действительно возрастает вслед за ростом массы тела коровы.
Рассчитаем доверительную зону (интервал), в которой с той или иной вероятностью заключены теоретические средние значения веса новорожденных. Критерий Стьюдента (нормированное отклонение) для уровня значимости α = 0.05, и числа степеней свободы df = п − 1 = 6 составит 2.45. Далее находим границы. Так, для значения x = 352 кг прогноз по уравнению регрессии равен Y = 25.56, а возможное отклонение средней составит:
t∙mY = 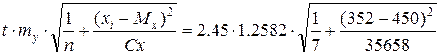 =
=
= 2.45∙0.81 = 1.98.
Отсюда находим границу доверительного интервала (табл. 16):
верхнюю: max Y = Yi + t∙mY = 25.56 + 1.98 = 27.54
и нижнюю: min Y = Yi − t∙mY = 25.56 − 1.98 = 23.58.
Средняя масса новорожденного теленка для коров весом 352 кг с вероятностью P = 0.95 должна находиться в диапазоне от 23.6 до 27.5 кг (рис. 14).
Регрессионный анализ позволяет проверить значимость и второго коэффициента уравнения регрессии, свободного члена b. Математический смысл свободного члена уравнения линии состоит в том, что этому значению равна функция (y) при условии, что аргумент равен нулю (x = 0):
y = ax + b= a∙ 0 + b = b.
В рамках регрессионного анализа рассматривается именно эта гипотеза Но: b = 0, т. е. что линия регрессии проходит через начало осей координат, точку пересечения осей координат, через нуль. Если гипотеза опровергается, значит, линия регрессии не пересекает ось ординат. Если гипотеза не опровергается, мы можем считать, что между признаками существует простая пропорция (Y = ax) и расчет коэффициента регрессии a упрощается: a = Σ(x∙y) / Σ x ². Нулевая гипотеза Но: b = 0 проверяется по критерию Стьюдента: t = (b − 0) / mb = b / mb ~ t (0.05, n −2), где mb – ошибка коэффициента b.
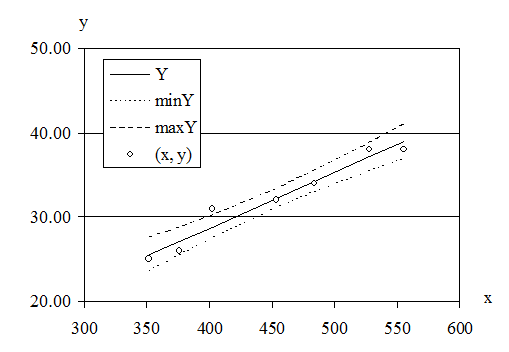
Рис. 14. Линия регрессии Y = 0.0657∙x+ 2.1347 и ее доверительный интервал
Ошибка второго коэффициента регрессии рассчитывается в два этапа. Сначала находим общую ошибку регрессионной средней (или остаточное стандартное отклонение), которая может вычисляться по-разному.
Точная формула для небольших выборок дает величину:
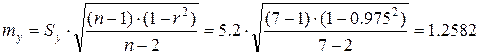 .
.
Общая точная формула показывает практически такой же результат:
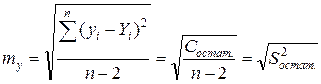
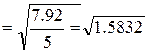 = 1.2582
= 1.2582
(величина Cостат. = 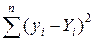 – это сумма квадратов разности между расчетными и реальными значениями признака, она найдена в табл. 16, внизу 7 графы, Cостат. = 7.92).
– это сумма квадратов разности между расчетными и реальными значениями признака, она найдена в табл. 16, внизу 7 графы, Cостат. = 7.92).
Теперь вычисляем ошибку коэффициента b:
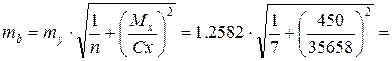 3.0359
3.0359
и критерий t Стьюдента: tb = b / mb = 2.419 / 3.0359 = 0.797.
Для уровня значимости α = 0.05 и числа степеней свободы df = n − 2 = 5 табличное значение составляет t (0.05, 5) = 2.57. Анализ показал, что критерий Стьюдента для свободного члена уравнения (0.797) оказался ниже табличного значения (2.57), т. е. коэффициент b значимо от нуля не отличается (при данном объеме собранных материалов). Это позволяет пересчитать коэффициент регрессии: a = Σ(x∙y) / Σ x ² = 0.071. Теперь можно пользоваться уравнением регрессии вида: Y = 0.071∙ x.
Оценить достоверности взаимодействия признаков можно и с помощью дисперсионного анализа (табл. 17). В этом случае общая дисперсия зависимого признака y (Cобщ.) разлагается на две составляющие – регрессионную дисперсию (изменчивость признака y, связанная с влиянием признака x, Срегр .) и случайную, или остаточную, дисперсию (изменчивость признака y, связанная с влиянием неучтенных случайных факторов, Состат . (рис. 14, табл. 17, 18).
 Общую сумму квадратов (Собщ . = Cy = Σ (yi − My) 2 = Σ yi 2 − (Σ yi)2 / n) находят непосредственно как сумму квадратов отличий между значением yi для каждой варианты и общей средней признака y. Остаточную сумму квадратов (Состат . = Σ (yi − Yi)2) находят также непосредственно как сумму квадратов отличий между значением yi для каждой варианты и значением, предварительно рассчитанным по уравнению регрессии Yi = axi + b (для соответствующих значений xi). Модельную сумму квадратов (Смод. = Σ (Yi − My)2) рассчитывают как разность между общей и остаточной (Смод . = Cобщ . − Cостат .).
Общую сумму квадратов (Собщ . = Cy = Σ (yi − My) 2 = Σ yi 2 − (Σ yi)2 / n) находят непосредственно как сумму квадратов отличий между значением yi для каждой варианты и общей средней признака y. Остаточную сумму квадратов (Состат . = Σ (yi − Yi)2) находят также непосредственно как сумму квадратов отличий между значением yi для каждой варианты и значением, предварительно рассчитанным по уравнению регрессии Yi = axi + b (для соответствующих значений xi). Модельную сумму квадратов (Смод. = Σ (Yi − My)2) рассчитывают как разность между общей и остаточной (Смод . = Cобщ . − Cостат .).
Рис. 15. Модель варианты в регрессионном анализе
Таблица 17
| Составляющие дисперсии | Суммы квадратов, С | Формулы расчета сумм квадратов | df | S ² | F |
| Регрессия | Срегр . = Σ(Yi − My)2 | Cобщ. − Cостат. | S 2 регр . = = 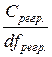 | 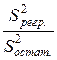 | |
| Отклонения вариант от линии регрессии | Состат . = = Σ(yi − Yi)2 | n − 2 | S 2 остат . = = 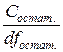 | F (0.05, 1, n −2) | |
| Общая (всего) | Собщ . = = Σ(yi − My)2 | (Σ yi 2 − Σ yi)2 / n= = Cy |
Таблица 18
| Составляющие дисперсии | С | df | S ² | F | |
| Регрессия | Срегр . = = Σ (Yi − Y)2 | 154.08 | S 2 регр . = = 154.08 | F = = 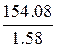 = = 97.3 = = 97.3 | |
| Отклонения вариант от линии регрессии | Состат . = = Σ (yi − Yxi)2 | 7.92 | S2остат . = = 1.58 | F (0.05, 1, 5) = 6.6 | |
| Общая (всего) | Собщ . = = Σ (yi − Y)2 |
Показателем «силы влияния признака на признак» служит коэффициент детерминации, отношение регрессионной суммы квадратов к общей сумме квадратов (принимает значения от 0 до 1): 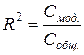
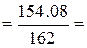 0.95. Между коэффициентом детерминации и коэффициентом корреляции существует простое соответствие: r =
0.95. Между коэффициентом детерминации и коэффициентом корреляции существует простое соответствие: r = 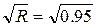 = 0.975.
= 0.975.
Построив таблицу дисперсионного анализа с помощью критерия Фишера можно проверить нулевую гипотезу Но: предсказания регрессионной модели в целом неадекватно описывают исходные данные, зависимости между признаками нет. Конструкция критерия исследует вопрос, превышает ли варьирование, учтенное моделью, случайное (остаточное) варьирование? Критерий Фишера вычисляется как отношение модельной и остаточной дисперсии:
F = S2мод . / S2остат . = 154.08 / 1.58 = 97.3.
Табличное значение F (0.05, 1, 5) = 6.6. Поскольку полученное значение критерия оказалось выше табличного, дисперсия реального признака y приближается по величине к дисперсии расчетных значений признака Y, т. е. существенно превышает (случайные) отличия между ними. Регрессионная модель в целом адекватно описывает исходные данные.
 2015-07-04
2015-07-04 2571
2571
