Криволинейная регрессия

В большинстве случаев связь биологических признаков не бывает линейной, они изме­няются либо с разной скоро­стью, либо в разных мас­штабах. Соответствен­но на графике форма такой связи отображается не прямой, а кривой линией. Примерами могут служить геометрическая прогрессия роста численности популяции в оптимальных условиях, различие скоростей роста разных частей тела, определяющее аллометрический характер зависимости признаков (лицевой отдел черепа растет более интенсивно, чем мозговой). В подобных случаях эффективнее использовать не уравнения прямой линии (у = ах + b), а разнообразные уравнения кривых линий, например, степенной, гиперболической, экспоненциальной, параболической, логистической и др.

Поскольку метод наименьших квадратов исходно ориентирован на линию (поиск уравнения линии, наименее удаленной ото всех эмпирических точек), прямой расчет уравнений кривых в рамках регрессионного анализа невозможен. Натурные данные необходимо предварительно «выпрямить», т. е. сделать возможным вычисление линейного уравнения регрессии с тем, чтобы потом из него получить уравнение криволинейной связи. Общий порядок регрессионного анализа для криволинейной зависимости следующий:

– преобразование исходных данных, «выпрямляющее» зависимость,

– расчет коэффициентов линейной регрессии преобразованных данных,

– проведение дисперсионного анализа, оценка значимости коэффициентов регрессии,

– обратное преобразование коэффициентов линейной регрессии для конструирования уравнения криволинейной регрессии.

Рассмотрим процесс поиска уравнения криволинейной регрессии на примере изучения зависимости веса печени прыткой ящерицы от длины ее тела (рис. 16).

Рассчитанное по исходным данным уравнение линейной регрессии имеет вид: у = 107. 9х − 404.2. И хотя коэффициент регрессии досто­верен (t = 7.6, α < 0.05) и коэффициент детерминации высок R ² = 0.866, это уравнение весьма приблизительно описыва­ет зависимость признаков – для наимень­ших наблюдаемых значений длины тела оно дает абсурдное (отрицательное) значение массы печени (107.9∙3.4 − 404.2 = −37.3 мг). Линейная модель не годится даже для интерполяции изучаемых данных. Гораздо успешнее справляется с подобной задачей степенная (аллометрическая) функция у = b x ^a.

0.765∙x3.07

∙ x 3.07

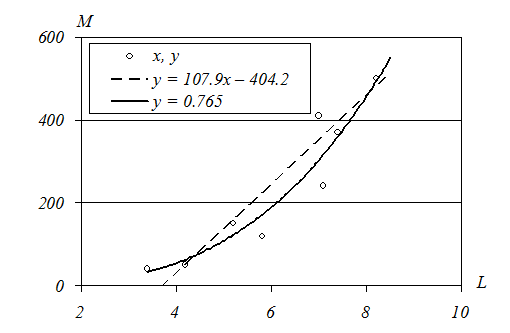
Рис. 16. Зависимость веса печени (M, мг) от длины тела (L, мм)

у ящериц

Для вычисления коэффициентов этого уравнения воспользуемся преобразованием: Y = lg y, X = lg x, B = lg b. После логарифмирования степенное уравнение приняло линейный вид: lg y = lg b + a ∙lg x или Y = B + aX. Теперь остается отыс­кать коэффициенты уравнения B и a, используя алгоритм метода наименьших квадратов (табл. 19).

Таблица 19

№	х	у	X = lg x	Y = lg y	X ²	Y ²	X∙Y	Y ’	(Y ’− Y)²	y ’
	3.4		0.531	1.60	0.282	2.567	0.85	1.517	0.00718
	4.2		0.623	1.69	0.388	2.886	1.06	1.799	0.01009
	5.2		0.716	2.18	0.513	4.735	1.56	2.085	0.00838
	5.8		0.763	2.08	0.583	4.323	1.58	2.23	0.02284
	7.1		0.851	2.38	0.725	5.665	2.03	2.5	0.01442
	7.0		0.845	2.61	0.714	6.827	2.21	2.481	0.01728
	7.4		0.869	2.57	0.756	6.596	2.23	2.556	0.00016
	8.2		0.914	2.69	0.835	7.284	2.47	2.693	0.00004
	8.5		0.929	2.78	0.864	7.758	2.59	2.741	0.00201
Σ	56.8		7.043	20.6	5.66	48.64	16.6		0.08239

Далее рассчитаем суммы, необходимые промежуточные значения и коэффициенты (расчеты выполнялись в среде Excel):

Σ Y = Σlg y = 20.6, Σ Y ² = Σ(lg y)² = 48.64, Σ X = Σlg x = 7.043,

Σ X ² = Σ(lg x)² = 5.659, Σ XY = Σ(lg x ∙lg y) = 16.577,

M_Y = Σ Y / n = 20.6 / 9 = 2.289, M_X = Σ X / n = 7.043 / 9 = 0.7826,

C _XY = Σ XY − (Σ X)∙(Σ Y) / n = 16.572 − 7.043∙20.602 / 9 = 0.45542,

C _X = Σ X ² − (Σ X)² / n = 5.655 − (7.04)² / 9 = 0.14816,

C _Y = Σ Y ² − (Σ Y)² / n = 48.638 − (20.601)² / 9 = 1.4823,

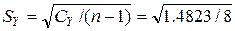= 0.4305,

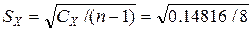= 0.1361,

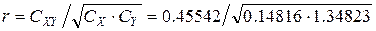= 0.9718,

a = C_XY / C_X = 0.45541 / 0.14815 = 3.0739,

B = M_Y − aM_X = 2.289 − 3.0739∙0.7826 = −0.11643.

Линейное уравнение для преобразованных данных имеет вид:

lg y = 3.07∙lg x + lg(−0.116) или Y' = 3.07∙ X − 0.116.

Это уравнение дает возможность рассчитать теоретические значения признака Y' (теоретические значения логарифмов массы печени), квадраты отклонений прогнозных значений от реальных: (Y' − Y)², а также их сумму Σ(Y' − Y)² = 0.08239.

Эта величина есть остаточная сумма квадратов; вместе с общей суммой квадратов Cy = C_{общ .} = 1.4823 она позволяет сформировать таблицу дисперсионного анализа (табл. 20): С_{мод .} = С_{общ .} − С_{остат .} = 1.4823 − 0.08239 = 1.39993.

Таблица 20

Составляющие дисперсии	С		df	S ²	F
Наклон модельной линии	Срегр . = = Σ (Y'i − MY)2	1.399		S2 регр . = 0.39993	F = = 118.9377
Отклонения вариант от линии	Состат . = = Σ (yi − Y'i)2	0.0824		S2остат . = 0.01177	F (0.05,1,7) = = 5.6
Общая (всего)	Собщ . = = Σ (yi − MY)2	1.482

Полученное значение F = 118 больше табличного (5.6), следовательно, дисперсия, обусловленная регрессией, достоверно больше случайной, т. е. признак Y действительно зависит от признака X, и линия регрессии адекватна исходным данным. Коэффициент детерминации больше, чем у линейной регрессии, и составляет: R ² = С_{регр .} / С_{общ .} = 1.399 / 1.4823 = 0.944.

Ошибка коэффициента криволинейной регрессии равна:

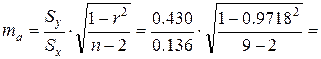0.281,

а критерий Стьюдента, проверяющий гипотезу Но: a = 0, составляет

t = a / m_a = 3.0739 / 0.281 = 10.9.

Полученное значение (10.9) больше табличного (t _{(0.05, 8)} = 2.31 для уровня значимости α = 0.05 и числа степеней свободы df = n − 2 = 8), коэффициент регрессии a значимо отличается от нуля; зависимость признака Y от X есть, причем очень тесная. Следует помнить, что при расчете ошибки коэффициента криволинейной регрессии используются стандартные отклонения для преобразованных (у нас – прологарифмированных) значений при­знаков.

В завершение выполним обратное преобразование второго коэффициента регрессии, свободный член равен:

b = 10 ^B = 10^−0.11643 = 0.764839.

Теперь уравнение регрессии принимает вид степенной зависимости:

у' = 0.765∙ x ^3.07.

Теоретические значения у ', рассчитанные по этому уравнению, гораздо ближе к исходным данным, что хорошо видно и на графике (рис. 16), и по большей величине коэффициента детерминации (0.94 > 0.87) (читателю несложно будет проделать все вычисления в среде Excel с помощью программы Регрессия – как для исходных, так и для преобразованных данных).

Аллометрическое уравнение (у' = 0.8 х ³) не только лучше описывает зависимость между признаками в статистическом плане, но и придает ей более ясный биологический смысл (масса печени = 0.8∙длина тела³). Как известно, объемные величины (объем, масса тела) пропорциональны кубу линейных промеров (длина тела). В свою очередь, вес печени и вес тела связаны прямой пропорциональной зависимостью. Так становится понятной наблюдаемая прямая пропорциональность веса печени кубу длины тела.