2015-07-04
300
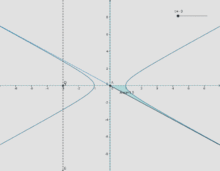
Ввиду соотношения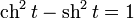 
гиперболические функции дают параметрическое представление гиперболы 
(
, 
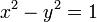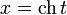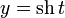). При этом аргумент 
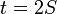, где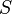 
— площадь криволинейного треугольника 
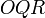, взятая со знаком «+», если сектор лежит выше оси 
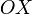, и «−» в противоположном случае. Очевидно, что и гиперболические функции определяются через этот параметр, например, уравнения гиперболического синуса в параметрической форме: 
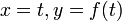, где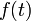 
— ордината точки гиперболы, соответствующей площади 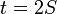. Это определение аналогично определению тригонометрических функций через единичную окружность, которое тоже можно построить подобным образом.
Важные соотношения
1. 
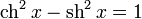(Тождество)
2. Чётность:
1. 
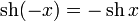
2. 
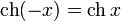
3. 
