Лабораторная работа N4
Цель работы вычисление спектров и построение графиков амплитудного и фазового спектров периодического сигнала.
Сведения из теории
Условие периодичности — x(t) = x(t+mT), где T — период, m - натуральное число, m= 1, 2,....
Любой периодический сигнал x(t) может быть представлен тригонометрическим рядом Фурье
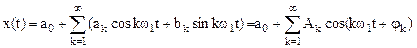 , (1.1)
, (1.1)
где 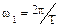 — угловая частота 1-й или основной гармоники;
— угловая частота 1-й или основной гармоники; 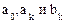 — коэффициенты разложения, вычисляемые по формулам:
— коэффициенты разложения, вычисляемые по формулам:
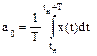 ;
; 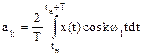 ;
; 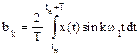 ; (1.1)
; (1.1)
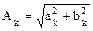 ;
; 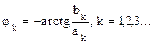 ,
,
где 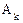 — амплитуда k-й гармоники;
— амплитуда k-й гармоники; 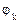 — фаза k-й гармоники;
— фаза k-й гармоники; 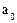 — среднее значение сигнала (постоянная составляющая);
— среднее значение сигнала (постоянная составляющая); 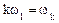 — угловая частота k-й гармоники;
— угловая частота k-й гармоники; 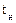 — момент времени, соответствующий началу периода.
— момент времени, соответствующий началу периода.
Зависимости 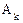 и
и 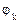 от частоты
от частоты 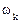 — это спектры амплитуд и фаз соответственно.
— это спектры амплитуд и фаз соответственно.
В некоторых случаях более удобна комплексная форма ряда Фурье
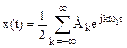 . (1.2)
. (1.2)
Коэффициенты 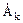 ряда (1.2) вычисляются по формуле
ряда (1.2) вычисляются по формуле
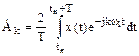 . (1.3)
. (1.3)
Формулы (1.2) и (1.3) — пара преобразований Фурье. Совокупность коэффициентов 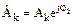 — комплексный спектр периодического сигнала x(t). Совокупность действительных величин
— комплексный спектр периодического сигнала x(t). Совокупность действительных величин 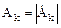 в зависимости от частоты — спектр амплитуд. Совокупность величин
в зависимости от частоты — спектр амплитуд. Совокупность величин 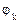 в зависимости от частоты — спектр фаз.
в зависимости от частоты — спектр фаз.
Ряд (1.2) удобно представлять в форме
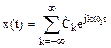 , (1.4)
, (1.4)
где 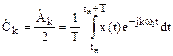 . (1.5)
. (1.5)
Типовые примеры
Задача 1.1.. Построить амплитудный спектр периодической последовательности идеальных прямоугольных импульсов z(t), график которой приведен на рис.1.1 на базе тригонометрического ряда Фурье.
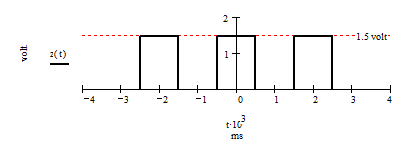
Рис.1.1
Ответ. При единице времени одна миллисекунда 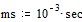 , номерах гармоник
, номерах гармоник 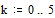 , амплитуде
, амплитуде 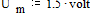 , периоде
, периоде 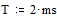 , частоте 1-й гармоники
, частоте 1-й гармоники 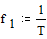 и k-й гармоники
и k-й гармоники 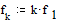 амплитудный спектр
амплитудный спектр
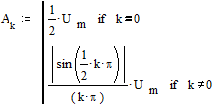 .
.
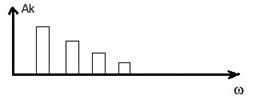
График амплитудного спектра в виде столбчатой диаграммы приведен на рис.1.2.
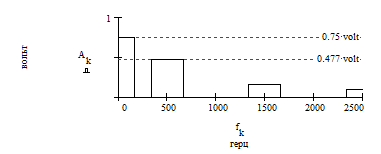
Рис.1.2
Задача 1.1.4. Найти амплитудный и фазовый спектры сигнала u(t) на выходе однополупериодного выпрямителя на основе комплексного ряда Фурье. График сигнала показан на рис.1.3.
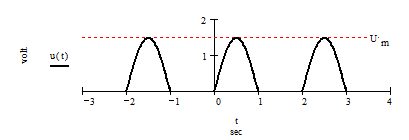
Рис.1.3
Ответ. Амплитудный спектр
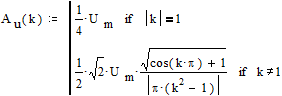 .
.
Фазовый спектр 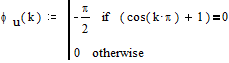 .
.
Вычисление коэффициентов ряда Фурье может быть выполнено по формулам (1.1.). Вычисление коэффициентов по этим формулам носит название непрерывного преобразования Фурье (НПФ).
Следует заметить, что даже для функций относительно простого вида интеграл от произведения заданной функции 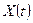 на
на 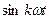 или
или 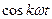 редко выражается через элементарные функции.
редко выражается через элементарные функции.
На практике часто приходится иметь дело с эмпирическими функциями, заданными дискретным рядом точек на конечном интервале. При спектральном анализе функций, заданных таким образом, приходится прибегать к так называемому дискретному преобразованию Фурье (ДПФ), которое сохраняет большинство свойств НПФ, но имеет ряд особенностей, которые будут обсуждены ниже.
Таким образом, задачей практического спектрального анализа является нахождение коэффициентов ряда Фурье функции, заданной в дискретной форме.
Пусть функция 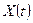 задана на некотором временном промежутке
задана на некотором временном промежутке 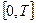 в дискретных точках
в дискретных точках 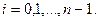 (Рис 1.4)
(Рис 1.4)
Определение коэффициентов 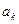 и
и 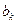 для последовательности x(i) численными методами производится по формулам
для последовательности x(i) численными методами производится по формулам
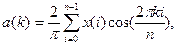
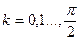 (1.6)
(1.6)
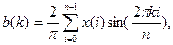
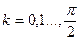 (1.7)
(1.7)
Переход от коэффициентов 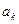 и
и 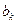 к последовательности
к последовательности 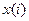 осуществляется в соответствии с выражением
осуществляется в соответствии с выражением
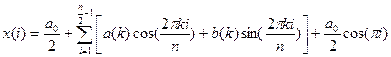 ,
,  =0,1,…,n-1 (1.8)
=0,1,…,n-1 (1.8)
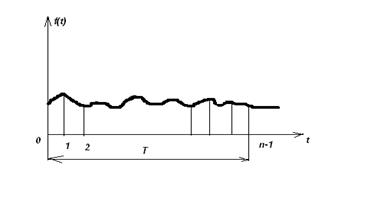
Рис. 1.4
В дискретном виде пара преобразования Фурье имеет вид:
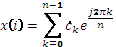 (1.9)
(1.9)
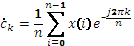 (1.10)
(1.10)
где k =0, 1, 2,.., n-1; i =0, 1, 2,.., n-1
Выражение (1.10) решает задачу гармонического анализа, т.е. нахождение комплексных коэффициентов 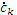 , а следовательно,
, а следовательно, 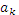 и
и 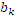 . Комплексные коэффициенты
. Комплексные коэффициенты 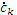 в формулах (1.9) и (1.10) связаны с амплитудами
в формулах (1.9) и (1.10) связаны с амплитудами 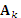 и фазами
и фазами 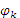 в тригонометрической форме записи ряда Фурье (1.1) следующими соотношениями
в тригонометрической форме записи ряда Фурье (1.1) следующими соотношениями
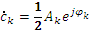
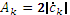
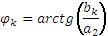
С коэффициентами 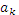 и
и 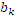 комплексные коэффициенты
комплексные коэффициенты 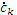 связаны формулами:
связаны формулами:
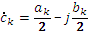 ;
; 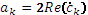 ;
; 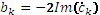 ;
;
Трудности практического спектрального анализа состоят в том, что по мере увеличения точек задания временной функции, количество вычислительных операций для нахождения коэффициентов Фурье возрастает нелинейно. Сокращение времени вычисления достигается применением быстрого преобразования Фурье (БПФ). Алгоритм БПФ сейчас реализован практически во всех средствах обработки данных. Подробное описание алгоритма и вычислительной процедуры БПФ имеется в методическом пособии по гармоническому анализу [ ]
Задание и методические рекомендации
- Задать периодический сигнал:
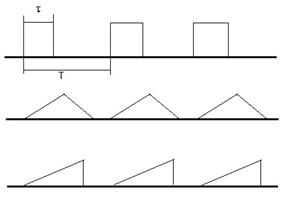
Длительность импульса 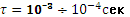 .
.
Скважность 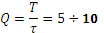
Амплитуда импульса 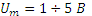
- Измерить N дискретных ординат на периоде
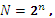 n=4, 5, 6 (не менее 16 ординат на периоде)
n=4, 5, 6 (не менее 16 ординат на периоде)
- Установить Exel и ввести в таблицу x(i)
i=0,.., n-1.
- Рассчитать спектр сигнала
Ø Сервис
Ø Анализ данных
Ø Анализ Фурье
Ø ОК
На экране: Диалоговое окно Анализ Фурье
- Установить входной интервал
- Ввести ссылку на левую верхнюю ячейку выходного интервала. Размер выходного интервала будет определён автоматически. Выходные значения представлены в формате:
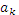 +i
+i 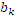 .
.
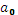
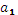 +i
+i 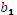
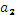 +i
+i 
…………..
5. Определить амплитуды гармоник 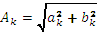 и построить амплитудный спектр.
и построить амплитудный спектр.
6. Построить фазовый спектр
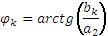
Оформление отчёта
В отчёте приведите ряд Фурье в тригонометрической и комплексной формах. Приведите формулы вычисления коэффициентов 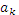 ,
, 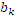 ,
, 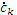 .
.
Рисунок временного сигнала, ординаты x(i).
Значения коэффициентов 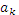 ,
, 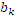 ,
, 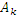 и фаз
и фаз 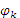 .
.
График амплитудного и фазового спектров.
Контрольные вопросы
- Что такое ряд?
- Ряд Фурье по произвольной системе функций
- Почему система функций должна быть ортогональной?
- Что означает понятие «частотное представление сигнала»
- Амплитудный и фазовый спектры сигнала.
- Основная тригонометрическая система функций.
- Как влияет длительность одиночного импульса на амплитудный спектр
Литература
1.1 Баскаков С.И. Радиотехнические цепи и сигналы. -М.: Радио и связь, 2000.
1.2 Гармонический анализ. Методическое пособие (электронное).
1.3 Ричард Рид. Основы теории передачи информации.- М.: Издательский дом Вильямс”,2005
 2015-07-04
2015-07-04 3583
3583








