Коэффициент вариации

Коэффициент вариации вычисляется следующим образом. Состав­ляется таблица, в которую вписываются результаты измерений и вычислений, например содержаний металла (табл. 12). Затем вы­числяется среднее арифметическое значение содержания (с_ср.)

с=∑с_i/n,

где сi,- — значение содержания в частной пробе;

п — число проб.

После этого производится вычисление разностей (Ас) каждого частного значения содержания от его среднего значения

Δc=c_i-c_ср.

Таблица 12 Пример вычисления коэффициента вариации

№ п/п	№ пробы	Содержание в пробах сi	Отклонение от среднего содержания Δc=ci-cср.	Квадрат откло­нения (Δc)2
		0,5	—0,3	0,09
		0,2	-0,6	0,36
		0,7	—0,1	0,01
		0,3	—0,5	0,25
		0,8	0,0	0,00
		0,9	+0,1	0,01
		1,1	+0,3	0,09
		0,6	—0,2	0,04
		0,9	+0,1	0,01
		1,2	+0,4	0,16
И		1,0	+0,2	0,04
		1,4	+0,6	0,36

Cср.=9,6/12=0.8

Δ=√1.42/11=0.34

Vв.=0,34/0,8*100=42,5%

Затем эти разности возводятся в квадрат (Δс²) и суммируются (∑Δс²). Далее определяется среднее кавдратическое отклонение («стандарт»)

Δ=√∑Δс²/n-1

Среднее квадратическое отклонение, отнесенное к среднему содержанию и выраженное в относительных процентах, дает значение коэффициента вариации (v_с):

Vc=Δ/ccр.*100%

Если велико число проб, то во избежание вычислительных операций по каждому значению содержания сначала производится группировка всех частных содержаний по отдельным классовым интервалам, затем составляется так называемая разносная решетка (табл. 13).

На основании этой разносной решетки составляется краткая подсчетная табл. 14. Вычислительные операции ведутся аналогично описанным выше и результаты вычислений коэффициента вариации по классовым группам такие же, как и по свободному ряду показателей признака.

Чем больше значение коэффициента вариации (чем выше степень изменчивости), тем большие погрешности могут быть при вычислении средних значений показателя. Поэтому при большей степени изменчивости число точек наблюдений должно быть достаточно большим. В этом легко убедиться, если рассмотреть формулу определения погрешности среднего арифметического (т):

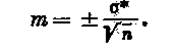
В относительных процентах погрешность выразится

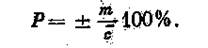
Таблица 13

Вспомогательная таблица для вычисления коэффициента вариации при большом количестве проб

Классовый интервал содержания, %	Среднее значение содержания классового интервала, %	Количество проб
0,01—0,10	0,05
0,11—0,20	0,15
0,21—0,30	0,25
0,31-0,40	0,35
0,41—0,50	0,45
0,51—0,60	0,55
0,61-0,70	0,65
0,71—0,80	0,75
0.81—0,90	0,85
0,91—1,00	0,95
1,01—1.10	1,05
1,11—1,20	1,15	g
1,21—1,30	1,25
1,31—1,40	1,35
1,41—1,50	1,45

Таблица 14 Пример вычисления коэффициента вариации при большом количестве проб

№ пп	Среднее содержание классового интервала (с)	Количество проб (n)	СП	Дс	Дс3	Дс2/ч
]	0,05		0,05	—0,75	0,5625	0,5625
	0,15		0,45	—0,65	0,4225	1,2675
з	0,25		1,00	—0,55	0,3025	1,2100
	0,35		2,45	—0,45	0,2025	1,4175
	0,45		3,60	—0,35	0,1225	0,9800
	0,55		6,60	—0,25	0,0625	0,8500
	0,65		8,45	—0,15	0,0225	0,2925
	0,75		15,00	—0,05	0,0025	0,0500
	0,85		26,35	+0,05	0,0025	0,0775
	0,95		18,05	+0,15	0,0225	0,4275
И	1,05		10,50	+0,25	0,0625	0,6250
	1,15		10,35	+0,35	0,1225	1,1025
	1,25		7,50	+0,45	0,2025	1,2150
	1,35		6,75	+ 0,55	0,3025	1,5125
	1,45		2,90	+0,65	0,4225	0,8450

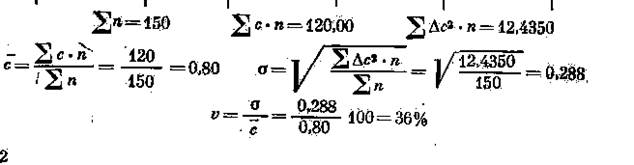
Если изобразить численность проб каждого классового интервала графически (рис. 39), то получится гистограмма, характеризующая распределение частот. Соединив вершины каждого классового интервала на гистограмме, получим кривую, которая назы­вается вариационной, или кривой распределения. Класс, обладающий наибольшим числом проб, называется модальным, а среднее значение показателя признака этого класса (в точке пересечения ординаты с осью абсцисс названа модой (М₀). Симметричная кривая распределения, или кривая Гаусса (рис. 40, а), отражает закон нормального распре­деления показателей признака (свойства).

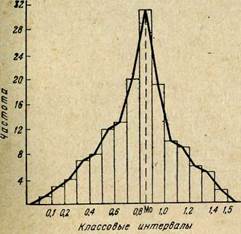
Рис. 39. Гистограмма и кривая распределения частот проб по классовым интервалам

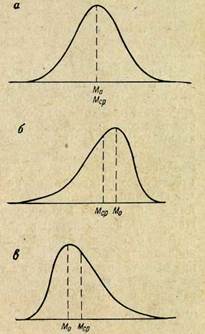
Рис. 40. Виды распределения показателя признака:

о — нормальное; 6 — асимметричное лево­стороннее; в — асимметричное правосто­роннее

Кривые распределения не всегда отвечают закону нормального распределения. На рис. 40, б, в показаны кривые распределения с левосторонней (отрицательной) и правосторонней (положительной) асимметрией. При правосторонней асимметрии среднее арифмети­ческое (М_ср) лежит правее моды (М_о) и, наоборот, — левее у кривых с левосторонней асимметрией.

Кривые распределения показывают, какие могут быть значения показателя признака и частоту таких значений, или, иными словами, вероятность появления таких значений. Если частоту содержания какого-либо классового интервала разделить на общее число проб, то получим величину, которая характеризует вероятность появления проб с таким содержанием. Иногда вероятность выражают в процен­тах. Для этого полученное значение умножают на 100%. Например, пробы с содержанием металла 0,7—0,8% были встречены в 20 слу­чаях из 150; следовательно, вероятность появления проб с таким содержанием будет равна 20: 150 = 0,133, или в относительных процентах — 13,3%.

Приведенные выше формулы математической статистики примени­мы при случайных явлениях (измерениях, анализах) и при условии,. что каждое измерение не связано какой-либо зависимостью друг с другом. В практике же геологоразведочных работ изменение мощно­сти или содержания обычно зависит от определенных геологических закономерностей. Часто можно наблюдать прямую или обратную зависимость содержания от мощности. Кроме того, показатель из­менчивости признака — коэффициент вариации — отражает только степень изменчивости, но не ее характер. Следует отметить также, что величина коэффициента вариации зависит не только от геологичес­ких особенностей месторождения, но и от ряда других факторов. Например, коэффициент вариации содержания полезного компонента зависит от способа отбора проб: чем больше объемы проб, тем меньше значения коэффициента вариации. Величина исследуемого участка при прочих равных условиях также влияет на величину коэффициен­та вариации: с увеличением участка в большинстве случаев увеличи­вается и значение вариационного коэффициента, поскольку происхо­дит объединение участков с различным характером оруденения и величинами средних содержаний, вследствие чего увеличиваются частные отклонения показателя признака от среднего.

Указанные выше недостатки не исключают возможности исполь­зования формул математической статистики в практике геологораз­ведочных работ, но в то же время требуют от геолога осторожного обращения с ними. Без соответствующего анализа геологических особенностей каждого конкретного месторождения применение фор­мул может привести к ошибочным выводам и рекомендациям.