1. Первообразная: определение и свойства.
2. Вычисление интегралов (неопределённого и определённого) непосредственным интегрированием.
3. Вычисление интегралов (неопределённого и определённого) заменой переменной.
4. Вычисление интегралов (неопределённого и определённого) интегрированием по частям.
5. Интегралы: 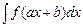 ,
, 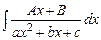 ,
, 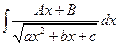 ,
, 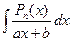 .
.
6. Вычисление интегралов вида 
7. Вычисление интегралов вида 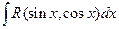 с помощью тригонометрических подстановок.
с помощью тригонометрических подстановок.
8. Вычисление интегралов вида: 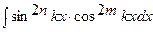 .
.
9. Вычисление интегралов вида 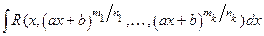
10. Вычисление интегралов вида 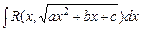 .
.
11. Вычисление несобственных интегралов 1-го и 2-го рода.
12. Вычисление площади плоской фигуры (в декартовых координатах).
13. Вычисление длины дуги плоской кривой (в декартовых координатах; в параметрическом виде).
14. Вычисление объёма тела вращения.
15. Нахождение среднего значения непрерывной на отрезке функции.
2012: Контрольная работа №2 по дисциплине «Математический анализ-2»
Темы: Ряды. Дифференциальные уравнения.
Вариант № 0
Темы: 1) Дифференциальные уравнения 1-го порядка (с разделяющимися переменными, однородное, линейное, Бернулли); 2) Дифференциальные уравнения высших порядков (простейшее, допускающее понижение порядка, линейные однородное и неоднородное с постоянными коэффициентами и правой частью специального вида); 3) Признаки сходимости и расходимости числовых рядов; 4) Радиус, интервал и область сходимости степенного ряда; 5) Разложение функций в ряд Тейлора.
| № | Задания | Ответы | Баллы |
| 1.1 | Для уравнения: 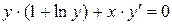
| ||
| а) установить тип ДУ; | ДУ с разделяющимися переменными | 0.1 | |
| б) найти общее решение. | 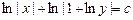
| 0.9 | |
| 1.2 | Для уравнения: 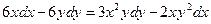
| ||
| а) установить тип ДУ; | ДУ с разделяющимися переменными | 0.1 | |
| б) найти общее решение. | 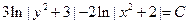
| 0.9 | |
| 1.3 | Для уравнения: 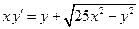
| ||
| а) установить тип ДУ; | Однородное ДУ 1-го порядка. | 0.1 | |
| б) найти общее решение. | 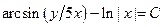
| 0.9 | |
| 1.4 | Для уравнения: 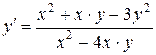
| ||
| а) установить тип ДУ; | Однородное ДУ 1-го порядка. | 0.1 | |
| б) найти общее решение. | 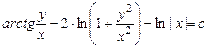
| 0.9 | |
| 2.1 | Для уравнения: 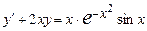
| ||
| а) установить тип ДУ; | Линейное ДУ 1-го порядка | 0.1 | |
| б) найти общее решение; | 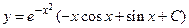
| 0.7 | |
в) найти частное решение, удовлетворяющее начальному условию 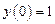 . .
| 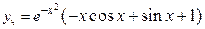
| 0.2 | |
| 2.2 | Для уравнения: 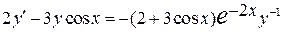
| ||
| а) установить тип ДУ; | Уравнение Бернулли. | 0.1 | |
| б) найти общее решение; | 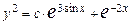
| 0.7 | |
в) найти частное решение, удовлетворяющее начальному условию 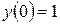 . .
| 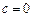 , , 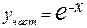
| 0.2 | |
| 3.1 | Найти общее решение простейшего ДУ второго порядка: 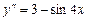
| 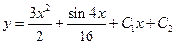
| |
| 3.2. | Для однородного ЛДУ 2-ого порядка с постоянными коэффициентами: 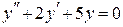
| ||
| а) найти общее решение; | 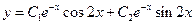
| 0.6 | |
б) найти частное решение, удовлетворяющее начальным условиям: 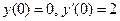 . .
| 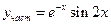
| 0.4 | |
| 3.3 | Для однородного ЛДУ 2-ого порядка с постоянными коэффициентами: 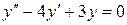
| ||
| а) найти общее решение; | 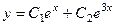
| 0.6 | |
б) найти частное решение, удовлетворяющее начальным условиям: 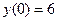 , , 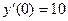 . .
| 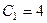 , ,  , , 
| 0.4 | |
| 3.4 | Соответствие ДУ 1-го порядка его названию:
1: 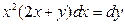 1: линейное
2: 1: линейное
2: 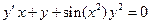 2: Бернулли
3: 2: Бернулли
3: 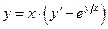 3: однородное
4: 3: однородное
4: 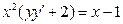 4: с раздел.перем.
В ответе указать пары, соответствующих друг другу ДУ и их названий. 4: с раздел.перем.
В ответе указать пары, соответствующих друг другу ДУ и их названий.
| 1-1 2-2 3-3 4-4 | |
| 4.1 | Для НЛДУ второго порядка с постоянными коэффициентами 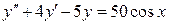
| ||
| а) найти общее решение однородного уравнения; | 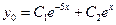
| 0.4 | |
| б) найти общее решение неоднородного уравнения. | 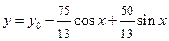
| 0.6 | |
| 4.2 | Для НЛДУ второго порядка с постоянными коэффициентами 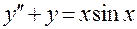
| ||
| а) найти общее решение однородного уравнения; | 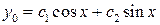
| 0.4 | |
| б) найти общее решение неоднородного уравнения. | 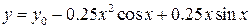
| 0.6 | |
| 5.1 | Для НЛДУ с постоянными коэффициентами 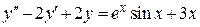
| ||
| а) найти общее решение однородного уравнения; | 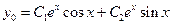
| 0.4 | |
| б) найти общее решение неоднородного ДУ (с точностью до неизвестных постоянных в частном решении). | 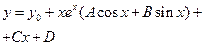
| 0.6 | |
| 5.2 | Найти общее решение ДУ: 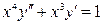
| 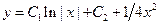
| |
| Исследовать сходимость числовых рядов и указать применяемые признаки (сравнения, Даламбера, радикальный и интегральный признаки Коши, достаточный признак расходимости): | |||
а) 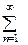 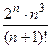
| сходится по признаку Даламбера, так как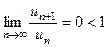 ; ;
| 0.5 | |
б) 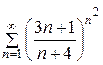
| расходится по радикальному признаку Коши, так как 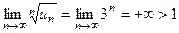 . .
| 0.5 | |
| 7.1 | Найти радиус, интервал и область сходимости степенного ряда: 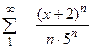
| 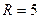 , , 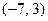 , , 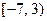
| |
| 7.2 | Найти первые три отличные от нуля члена разложения функции 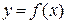 в ряд Тейлора в окрестности точки в ряд Тейлора в окрестности точки 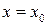 : : 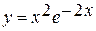 , , 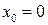 . .
| 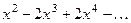
|
 2015-07-04
2015-07-04 278
278






