Метод половинного деления (дихотомии)

Общие положения

Решением или корнями уравнения Y(x)=0, называются такие значения аргумента х, при которых значение функции Y(x) становится равным нулю (равенство обращается в верное тождество). Только 2 класса уравнений – линейное ax + b = 0 и квадратное ax² + bx + c = 0 – имеют в общем случае аналитическое решение в виде формул. Все остальные классы уравнений имеют аналитические решения только в некоторых частных случаях.

В данной лабораторной работе мы познакомимся с численными методами нахождения корней для любых классов уравнений. При этом определять значение корня мы будем с некоторой заданной точностью e.

Вычисление корня нелинейного уравнения осуществляется в 2 этапа:

1 этап. Определение промежутков локализации [a, b]. Промежуток локализации [a, b] это такой промежуток обязательно есть корень функции, причем только один. Определение промежутков локализации выполняется с помощью построения таблицы значений и графика функции;

2 этап. Уточнение корней из выбранных промежутков локализации. На этом этапе применяются методы метод половинного деления (дихотомии), касательных (Ньютона), хорд и другие.

Этап.

Промежуток [a, b], на котором следует искать корень функции должен удовлетворять 2 условиям:

- функция Y(x) должна быть непрерывна на этом промежутке [a, b]:

- значения функции Y(x) на концах промежутка в точках a и b должны иметь разные знаки Y(a) * Y(b) < 0

Рассмотрим уравнение x³ -5x + 3 = 0. функция Y(x) = x³ -5x + 3 является непрерывной при любом х, так что первое условие выполняется всегда. Для определения промежутков, где функция меняет знак, построим таблицу значений функции. См. рисунок 1.

X	Y(x)=x³-5x +3
-3	-9
-2.5	-0.125
-2
-1.5	7.125
-1
-0.5	5.375

0.5	0.625
	-1
1.5	-1.125

Рис. 1

Поскольку на промежутке от -2.5 до -2 функция Y(x) поменяла знак, (Y(-2.5)=-0.125, Y(-2.0)=5) и функция непрерывна, то где-то на этом промежутке она принимает значение 0, то есть на этом промежутке у функции Y(x) = x³ -5x + 3 есть корень. У кубической функции должно быть 3 корня, что и обнаруживается при дальнейшем анализе таблицы.

На рисунке 2 представлен график этой функции, иллюстрирующий промежутки локализации корней.

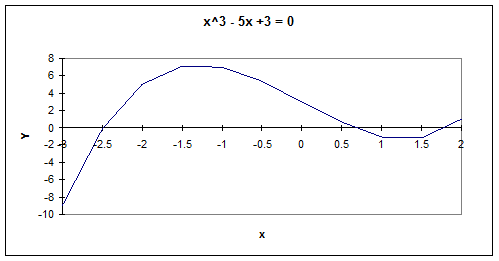
Рис. 2

Рассмотрим другой пример: tg(x) – x + 2 =0, левую часть уравнения обозначим Z(x)= tg(x) – x + 2. Как известно, tg(x) имеет разрывы в точках x= ±p ±pn. Построим таблицу значений функции Z(x), как показано на рисунке 3.

x	tg(x)-x+2
-2.5	5.247
-2	6.185
-1.5	-10.601
-1	1.443
-0.5	1.954
	2.000
0.5	2.046
	2.557
1.5	14.601
	-2.185
2.5	-1.247
	-1.143

Рис. 3.

Первое изменение знака функции Z(x) мы видим на промежутке [-2.0, -1.5], однако в точке x= -p/2 = -1.5759 имеется разрыв функции, нарушено условие непрерывности, поэтому на промежутке [-2.0, -1.5] корня нет. На промежутке [-1.5, -1.0] опять изменился знак функции, при чем на этом промежутке функция Z(x) непрерывна, поэтому промежуток [-1.5, -1.0] является промежутком локализации и содержит корень функции. Дальнейший анализ таблицы значений показывает, что на промежутке [1.5, 2.0] снова происходит смена знака функции, но в точке x= p/2 = 1.5759 имеется разрыв функции, следовательно корня на этом промежутке нет.

Рисунок 4 показывает график функции Z(x)= tg(x) – x + 2. На рисунке видно, что на промежутках [-2.0, -1.5] и [1.5, 2.0] не может быть корней функции Z(x).

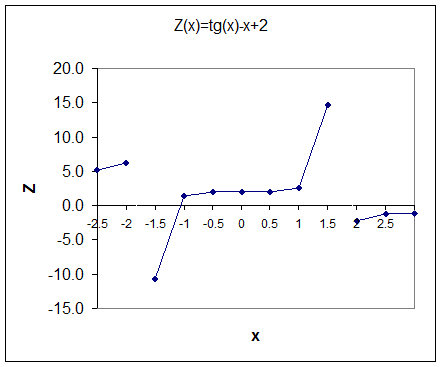
Рис. 4.

Этап.

Уточнение корней из выбранных промежутков [a, b].

Рассмотрим 3 метода, позволяющих определить корень с заданной точностью e: метод половинного деления или дихотомии, метод касательных или Ньютона и метод хорд.

Метод половинного деления (дихотомии)

Этот метод заключается в последовательном делении промежутка [a, b]пополам и отбрасывании той части промежутка, где заведомо не может быть корня.

Пусть [a, b] это промежуток локализации корня уравнения Y(x)=0, тоесть функция непрерывна на этом промежутке и имеет разные знаки в точках a и b,например,Y(а) <0, Y(b) >0 как на рисунке 5. Алгоритм метода заключается в следующих шагах:

Шаг 1. Найдем среднюю точку промежутка [a, b] ;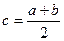

Шаг 2. Вычислим значение функции в точке с Y(с);

Шаг 3. Сравним значение функции в точке с Y(с) со значением функции в точке а Y(а), если оба значения отрицательны или оба значения положительны Y(а) * Y(с) > 0, то на левой половине отрезка от а до с корня нет (вспомним, что функция непрерывна), эту часть отрезка можно отбросить и дальше рассматривать правую половину отрезка промежуток [с, b], обозначив его как. промежуток[a, b]. То есть если Y(а) * Y(с) > 0, то точка а переносится в точку с: с=а. Если же в точках а и с функция имеет разные знаки Y(а) * Y(с) < 0, то корень находится между точками а и с, на левой половине отрезка [a,с], а правую половину [с, b] можно дальше не рассматривать. То если есть Y(а) * Y(с) < 0, то точка b переносится в точку с: с=b.. В результате нам удалось уменьшить длину исходного промежутка локализации корня в 2 раза, отбросив левую или правую половину отрезка. Из-за этого метод и называют методом половинного деления или дихотомии. Рисунок 5 иллюстрирует схему уменьшения длины отрезка локализации корня, знаки функции обозначены Å и Ө.

Попробуем отобразить указанные действия с помощью блок-схемы, что в дальнейшем поможет нам написать условные операторы.

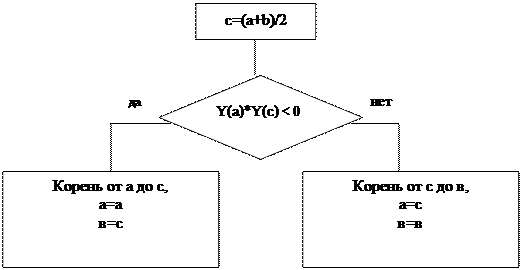
Шаг 4. Уменьшать таким образом длину промежутка [a, b] будем до тех пор, пока она не станет меньше заданной точности e, то есть как только получим |b-a|<=e, то будем считать, что корень найден и равен с.

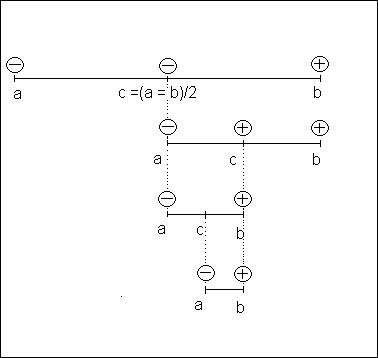
Рис. 5

Численный пример.

Найдем корень уравнения x³ -5x + 3 = 0 из промежутка [1.5, 2.0] с точностью e=0.002

Для этого в Excel потребуется создать следующую таблицу 1:

В ячейках A20, B20 находятся значения a=1.5 и b=2.0, найденные на этапе 1, в ячейке C20 вычислено значение средней точки с промежутка [a, b], в ячейках D20, E20 и F20 вычислены значения функции Y(a), Y(b), Y©. В ячейке G20 введена формула для сравнения длины промежутка с заданной точностью e и вывода сообщения о том, что корень найден (шаг 4). Для выполнения шага метода дихотомии надо в ячейках A21 и B21 ввести формулы в соответствии с шагом 3. Диапазон C21: G21 скопировать из C20: G20. Строка 22 и все последующие скопировать из соответствующего диапазона A21:G21, до появления сообщения " Корень найден”.

Таблица 1

=ЕСЛИ(D20*F20<0;A20;C20)

=ЕСЛИ(D20*F20<0;C20;B20)

ЕСЛИ(ABS(B20-A20)<=0.002; ”КОРЕНЬ НАЙДЕН”; ABS(B20-A20))

=(B20 + A20)/2

Y(a)

Y(b)

Y(с)

b-a

1.5

1.75

-1.125

-0.390625

0.5

1.75

1.875

-0.390625

0.21679688

0.25

1.75

1.875

1.8125

-0.390625

0.216797

-0.1081543

0.125

1.8125

1.875

1.84375

-0.108154

0.216797

0.04891968

0.0625

1.8125

1.84375

1.82813

-0.108154

0.04892

-0.0309563

0.0313

1.828125

1.84375

1.83594

-0.030956

0.04892

0.00864553

0.0156

1.828125

1.8359375

1.83203

-0.030956

0.008646

-0.0112392

0.0078

1.832031

1.8359375

1.83398

-0.011239

0.008646

-0.0013178

0.0039

1.833984

1.8359375

1.83496

-0.001318

0.008646

0.0036586

КОРЕНЬ НАЙДЕН

Рисунок 6 иллюстрирует приведенную таблицу. Над отрезком локализации приведены значения функцииY, под отрезком – значения величин a, b, c.

Рис. 6

Только для студентов дневного отделения

Создание пользовательской функции для вычисления корня функции из заранее определенного отрезка [a, b] точностью e (eps). Перейти в интегрированную среду разработки приложений Сервис ®Макрос ® Редактор VBA. Добавить стандартный модуль Insert ® Module. Сначала следует написать функцию, определяющую левую часть уравнения. Для рассмотренного выше примера x³ -5x + 3 = 0 эта функция будет иметь вид:

Function F(x)

F = x^3 -5 * x + 3

End Function

Функция, реализующая метод дихотомии выглядит следующим образом:

Function Dixotomia(a as double, b as double, eps as double)

Dim i as Integer ‘ I – количество итераций

If F(a) * F(b) > 0 Then

MsgBox ("Неправильно выбран промежуток [a, b]")

Exit Function

End If

i = 0

c = (a + b) / 2