2015-07-04
264
НА первом этапе уже определен промежуток локализации корня [a, b], такой, что на этом промежутке есть только один корень уравнения Y(x)=0.
Шаг 1. Проводим прямую (хорду) между точками с координатами (a, Y(a)) и (b, Y(b)). Выведем уравнение этой прямой g=k∙x + m:
g(b) = k ∙b + m (1)
g(a) = k ∙a + m (2)
Тогда
(3)
Подставим полученное для k выражение в (1) и выведем формулу для m.
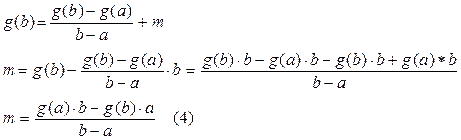
Теперь, определив коэффициенты уравнения прямой k m можно вычислить точку пересечения хорды с осью абсцисс x0, в которой g(x0)=0:
См. рис. 7 и рис. 8.
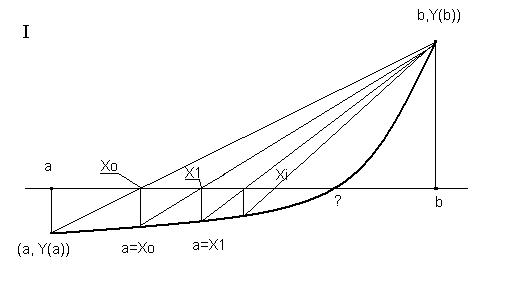
Рис. 7
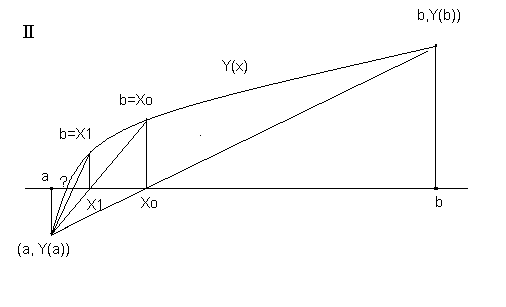
Рис. 8
Шаг 2. Затем сравним знаки функции Y(x) в точках а и x0 Y (а) и Y(x0).
Если знаки функции одинаковы Y(а)∙Y(x0) > 0, то на промежутке от а до x0 корня нет, дальше будем рассматривать промежуток [x0, b] и следующую хорду нужно провести между точками с координатами (x0, Y(x0)) и (b, Y(b)). Точку а переносим в x0. См. рис.7.
Если же, как на рис.8, Y(а) и Y(x0) имеют разные знаки, то есть Y(а)∙Y(x0) < 0, то дальше следует рассматривать промежуток [a, x0]. Следующую хорду надо провести между точками (a, Y(a)) и (x0, Y(x0)). Точку b переносим в x0.
|
|
|
Выбор точки а или b, из которой следует строить следующую хорду, можно также осуществить с помощью знака второй производной Y”(x). Если знак Y(b) и Y’’(b) совпадают (Y(b)∙Y’’(b) > 0, то хорды следует строить из точки b (рис 8. случай II), в противном случае из точки а (рис.7, случай I).
Эти действия можно представить в виде блок-схемы, показанной на рис. 9
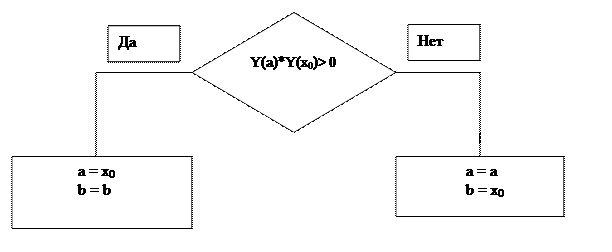
Рис. 9
Шаг 3. Следующее приближение к корню Y(x) x1 вычислим по формуле, аналогичной (5)
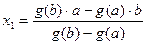и сократим длину промежутка [a, b] как на 2-ом шаге (рис.9).
Шаг 4. Продолжать вычисление x2, x3,….xi до тех пор, пока не выполнится условие
│xi – xi-1│≤ e (6)
Как только условие (6) выполнится, будем считать, что xi это корень функцииY(x), найденный с точностью e.
Численный пример.
Рассмотрим функцию x3 -5∙x + 3 = 0. Один из промежутков локализации -[1.5, 2], точность e=0.01
Вычисления приведены в таблице 2.
Шаг 1. Вычислим значения Y(a), Y(b), затем x0 по формуле (5) и Y(x0).
Шаг 2. Поскольку Y(a) и Y(x0) имеют одинаковый знак, то согласно блок-схеме на рис. 9, a = x0, b = b.
Шаг 3. Вычислим значения Y(a), Y(b), затем x1 по формуле (5) и Y(x1). Отметим, что │Y(x1)│ < │Y(x0)│.
Шаг 4. Проверим выполнение условия (6): x1 – x0 =0.0581 >e, поэтому продолжаем вычисления для x2, x3.
Разность между x3 и x2 (│x3 - x2│= 0.009) становится меньше заданной точности e = 0,01, следовательно корень найден и равен 1.8332.
Таблица 2
| i | a | b | xi | Y(a) | Y(b) | Y(xi) | │xi–xi-1│ |
| 1.5 | (1*1.5-1.125*2)/(1+1.125) =1.7647 | -1.125 | -0.328 | ||||
| 1.7647 | (1*1.7647-0.328*2)/(1+0.328) =1.8228 | -0.328 | -0.0575 | 0.2647 | |||
| 1.8228 | (1*1.8228-0.0575*2)/(1+0.0575) =1.8324 | -0.0575 | -0.00913 | 0.058 | |||
| 1.8324 | 1.8332 | -0.00913 | -0.00143 | 0.009 |
В таблице 3представлено решение в Excel с точностью 0.0005
|
|
|
В колонке A указывается номер итерации I, в ячейках AB78и D78 - границы промежутка локализации корня [a,b], в колонках E,F,G – значения функции Y в точках a, b, xi соответственно, в ячейках B80, C80 и ниже в этих колонках записывается условный оператор, соответствующий блок-схеме на рис.9. В колонке H вычисляется длина отрезка [Xi-Xi-1] на каждом шаге.
Таблица 3
| A | B | C | D | E | F | G | H | |
| 
| |||||||
| ||||||||
| 
| 
| ||||||
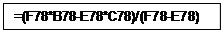
| i | a | b | Xi | Y(a) | Y(b) | Y(Xi) | Xi-Xi-1 | |
| 1.5 | 1.76471 | -1.125 | -0.32791 | |||||
| 1.76471 | 1.82281 | -0.32791 | -0.05752 | 0.26471 | ||||
| 1.82281 | 1.83245 | -0.05752 | -0.00913 | 0.05810 | ||||
| 1.83245 | 1.83396 | -0.00913 | -0.00143 | 0.00964 | ||||
| 1.83396 | 1.83420 | -0.00143 | -0.00022 | 0.00152 | ||||
| 1.83420 | 1.83424 | -0.00022 | -3.5E-05 | 0.00024 |
Так как в строке 84 длина отрезка [Xi-Xi-1] оказалась равной 0.00024 что меньше точности e=0.0005, то полученное в ячейке В84 значение X=1.83420 является корнем уравнения, вычисленным с точностью e=0.0005.
