В большинстве практических задач оптимизации объекта экстремум функционала качества обеспечивается при управлении, имеющем разрывы 1-го рода.
При этом координаты объекта также могут иметь разрывы 1-го рода, положение и число которых не известно.
Решение таких задач методом классического вариационного исчисления проблематично, поэтому используют принцип максимума Понтрягина.
Сущность принципа максимума:
При заданной модели объекта в форме системы уравнений Коши и заданных ограничениях на управление 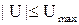 следует найти вектор оптимальных управляющих воздействий, которые обеспечивают минимум функционала качества. Для решения задачи вводится дополнительная функция ψ:
следует найти вектор оптимальных управляющих воздействий, которые обеспечивают минимум функционала качества. Для решения задачи вводится дополнительная функция ψ:
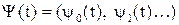 и записывается функция Гамильтона для неклассической вариационной задачи:
и записывается функция Гамильтона для неклассической вариационной задачи:
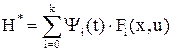
Оптимальное управление находится по частной производной:
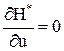
Каноническое уравнение Гамильтона для решения задачи записывается в следующей форме:
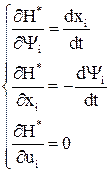
Если существует оптимальное управление, принадлежащее к классу допустимых управлений 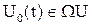 , то соответствующая этому управлению функция должна проходить через фиксированные начальную и конечную точки
, то соответствующая этому управлению функция должна проходить через фиксированные начальную и конечную точки 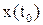 и
и 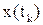 .
.
Теорема Понтрягина:
для того, чтобы управление было оптимальным, необходимо существование такой ненулевой вектор-функции ψ(t), существующей в силу системы уравнений Гамильтона и соответствующих функций x(t) и u(t), которая в интервале времени 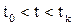 при оптимальном управлении обеспечит максимум Н*-функции.
при оптимальном управлении обеспечит максимум Н*-функции.
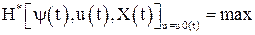
Причем в конечный момент времени 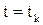 Н*-функция равна нулю:
Н*-функция равна нулю:
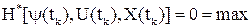
Наиболее удобно решать этим методом задачи на оптимальное быстродействие.
Принцип максимума сводит решение задачи к решению в (2n+r+2)-мерном пространстве дифференциальных уравнений.
В большинстве случаев 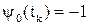 . в этом случае Н*-функцию можно записать следующим образом при функционале качества, определяющем максимальное быстродействие:
. в этом случае Н*-функцию можно записать следующим образом при функционале качества, определяющем максимальное быстродействие:
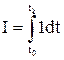
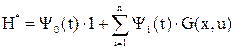 ,
,
где G – система уравнений объекта в форме Коши.
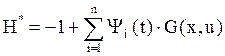
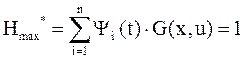
На основании принципа максимума для линейных объектов управление можно выбирать:
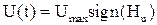 – релейное управление
– релейное управление
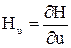
Из принципа максимума следует, что оптимальным по быстродействию является релейное управление, но не обычное, а с принудительным переключением реле.
В этом случае в системах оптимального по быстродействию системах схему управляющего устройства можно представить следующим образом:
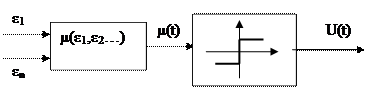
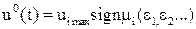
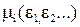 - функция переключения реле в зависимости от ошибки ее производных (она может быть записана в форме функции фазовых координат
- функция переключения реле в зависимости от ошибки ее производных (она может быть записана в форме функции фазовых координат 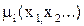 ).
).
 2015-07-04
2015-07-04 687
687








