Координатные системы. Геометрические преобразования

Прежде чем приступить к обсуждению механизмов преобразования изображения, дадим определение условий фиксации положения, дающих возможность показать соотношения между объектами (элементами) до и после выполнения преобразований.

Система правил, соотношений и изобразительных (графических) средств, позволяющая задать (определить) положение объекта внимания на плоскости или в пространстве, определяется как система отсчета, система координат (КС), по которой каждой точке пространства ставится в соответствие набор чисел (координат). Число координат, которые требуются для описания положения точки, определяет размерность пространства и соответственно наличие двухмерной и трехмерной графики. Двухмерная графика использует два понятия – высота и ширина и не вызывает особых затруднений при работе с изображением. В понятии трехмерная графика заложено указание на то, что придется работать с тремя пространственными измерениями – высотой, шириной и глубиной. Не вдаваясь в тонкости понятия “трехмерная графика”, отметим, что при работе с графическими средствами компьютерной графики необходимо помнить - созданные изображения реальных объектов существуют только в памяти компьютера. Они не имеют физической формы, поскольку это не что иное, как совокупность математических уравнений и движение электронов в микросхемах. А так как эти объекты не могут существовать вне компьютера, то единственным способом их увидеть в реальном свете, является добавление новых уравнений, описывающих условия освещения и точки зрения.

Основным отличием двухмерной графики от трехмерной является полное отсутствие у двухмерных объектов (изображений) третьей координаты – глубины, величины, характеризующей пространственные свойства объекта. Рисунки на плоскости характеризуются только шириной и высотой. И если ваше изображение таково, что создает иллюзию наличия третьей компоненты, то любая попытка взглянуть на объект с иного ракурса всегда будет связана с необходимостью перерисовывания объекта заново.

Если при моделировании трехмерные объекты приобретают координату глубины, то однажды нарисовав такие объекты, потом имеется возможность рассматривать их под любым углом зрения, не перерисовывая.

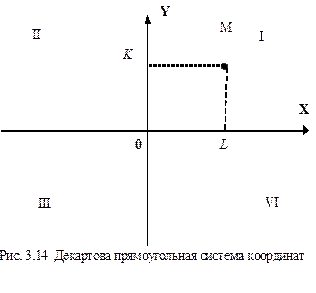Положение каждой точки в пространстве определяется тройкой чисел – координатами (шириной, высотой и глубиной). Таким образом, через каждую точку можно провести три координатные оси виртуального пространства. Координатная ось – это воображаемая линия пространства, определяющая направление изменения координаты. Точка пересечения трех осей, имеющая координаты (0,0,0) – это точка начала координат.

В машинной графике в зависимости от характера решаемых задач, от структуры представления изображений и от процесса обработки графических данных, используются различные координаты:

мировые;

полярные, цилиндрические, сферические;

относительные;

пользователя;

физические;

нормализованные;

афинные;

однородные.

Мировой координатой называют независимую от устройства декартову координату, используемую в прикладной программе при задании графических входных и выходных данных. Будем говорить, что на плоскости задана декартова прямоугольная система координат, если определена пара взаимно перпендикулярных осей и при этом обусловлено какая из этих осей является осью ординат, какая - осью абсцисс, а также единичный (масштабный) отрезок по осям. На рис. 3.14 изображена декартова система координат и определенная на ней точка M. Опустим из точки M перпендикуляры на оси OX и OY. Точки пересечения этих перпендикуляров с осями координат обозначены соответственно L и K. Абсциссой точки M называется отрезок 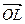оси OX, а ординатой – величина отрезка 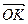оси Y. Пару чисел x и y, где x= 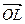, y= 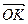называют координатами точки M в выбранной системе координат. Тот факт, что точка M имеет координаты x и y записывается так: M(x,y). При этом сначала пишется абсцисса, а затем ордината точки M.

Таким образом, каждой точке M плоскости соответствует пара действительных чисел (x,y) – координаты этой точки. Наоборот, каждой паре действительных чисел (x,y) соответствует, и при том только одна, точка M плоскости, для которой эти числа будут ее координатами.

Следовательно, введение на плоскости декартовой прямоугольной системы координат позволяет установить взаимно однозначное соответствие между множеством точек на плоскости и множеством пар[1] действительных чисел на плоскости. Это соответствие дает возможность сводить изучение множеств точек на плоскости к изучению множеств пар действительных чисел, то есть, применять к изучению вопросов геометрии алгебраические методы. Это же соответствие дает возможность давать геометрическую интерпретацию некоторым вопросам алгебры и других дисциплин.

Рассматривая прикладной аспект КС, необходимо отметить следующее. Поскольку координаты по своей природе являются безразмерными, позиционирование объектов выполняется в единицах, которые являются естественными для данного приложения и пользователя. Например, требуется показать график помесячного выхода продукции в течение года. Координаты в этой КС (x – месяц; y – выход продукции) называются координатами пользователя, а поскольку они позволяют задавать объекты в двухмерном и трехмерном мире их также называют глобальными координатами.

Если в рассматриваемом векторном пространстве не предполагается возможным сравнение длин единичных векторов (орт), |e₁|, |e₂|, |e₃|, то такое пространство называется аффинным. Аффинное векторное пространство позволяет изучать общие свойства фигур, изменяющиеся при произвольном преобразовании системы координат. Аффинная и декартова системы координат на плоскости устанавливают взаимно однозначное соответствие между точками и координатами.

Аффинная или декартова система координат называется правой, если совмещение положительной полуоси х с положительной полуосью у осуществляется поворотом оси Ox в направлении, противоположном направлению движения часовой стрелки на угол, меньший p. В противном случае система координат называется левой.

Если отрезки равны (случай метрического векторного пространства), а угол между осями ¹90⁰ КС называется косоугольной. То есть кроме декартовой КС существуют и другие системы координат, позволяющие определить положение точки на плоскости (пространстве) с помощью пар (троек) действительных чисел[2]. К таким КС относится, например, полярная система координат.

Полярная система координат. Определим на плоскости точку O и проходящую через нее ось OP. Точка O назовем полюсом, а полуось (луч), выходящую из точки O в положительном направлении[3], - полярной осью. Задание полюса полярной оси OP и единичного (масштабного) отрезка OE определяет на плоскости полярную систему координат. Полярным радиусом r любой точки M называется длина отрезка 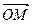. Полярным углом j точки M называется угол наклона направленного отрезка 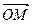к полярной оси OP. Угол j определяется с учетом знака и с точностью до слагаемого вида 2kp, гдe k – целое число.

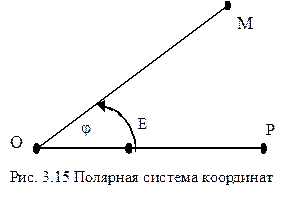Числа r и j, полярный радиус и полярный угол точки M, называются полярными координатами. Точка с полярными координатами обозначается так: M(r,j) или (r,j).[4]

Таким образом, задание любой пары действительных чисел (r,j), ³ 0 позволяет построить на плоскости одну точку M, для которой эти числа являются ее полярными координатами.

При создании изображений достаточно часто приходится пользоваться одновременно декартовыми прямоугольными и полярными координатами точек. Практический интерес представляют формулы, позволяющие по декартовым координатам рассчитывать полярные координаты и наоборот.

Пусть точка M произвольная точка плоскости, x и y – ее декартовы координаты, r,j - полярные. Так как

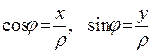
то

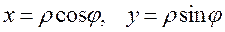(1)

Формулы (1) выражают прямоугольные декартовы координаты точки M через полярные координаты.

Далее, при любом положении точки M

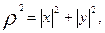то есть, 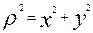, следовательно

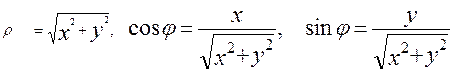(2)

Формулы (2) позволяют определить полярные координаты точки M по ее декартовым координатам. Если точка M не лежит на оси OY, то из формул (2) следует соотношение

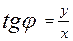
Физической координатой считают координату, заданную в системе координат, которая зависит от устройства.

Нормализованной координатой называют координату, заданную в промежуточной, независимой от устройств, системе координат и нормированную относительно некоторого диапазона, обычно от 0 до 1. При этом изображение, выраженное в нормализованных координатах, располагается в одной и той же относительной позиции при визуализации на любое устройство. Нормализованные координаты используются в случае, если область трехмерного пространства, ограниченная кубом, со стороной h отображается в ту же область, ограниченную кубом со стороной b', при этом используется нормирующий множитель, делением на который получают нормализованные координаты. Координаты мировой системы иногда приводятся к нормализованному виду.

Приборная система координат всегда нормирована. Координаты обычно задаются в десятичных долях в диапазоне от О до 1 или в целых единицах, например, растра экрана дисплея (размер 1024 X 10*4 единиц растра).

Однородная система координат широко применяеся в машинной графике и позволяет n-мерный объект представить в (n +1) - мерном пространстве, путем добавления еще одной координаты - скалярного множителя. Однородные координаты являются основными в проективной геометрии, в машинной графике они удобный искусственный прием, позволяющий линеанизировать перспективные изображения. Однородные координаты дают возможность записывать несобственные (бесконечно удаленные) точки пространства, а также выражать аффинные преобразования в удобной матричной форме, избегая переполнения разрядной сетки ЭВМ за счет нормализации чисел.

Определяются однородные координаты следующим образом. Пусть на плоскости заданы система аффинных координат и произвольная точка Р с координатами (х, у). Введем в рассмотрение систему координат, в которой для описания вектора положения точки вводится третья компонента. Назовем однородной системой координат любую тройку одновременно не равных нулю чисел а₁, а₂, а₃, связанных соотношением

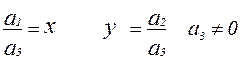
При решении задач компьютерной графики однородные координаты обычно вводятся так: произвольной точке M(x, y) на плоскости ставится в соответствие точка M’(x, y) в пространстве. Заметим, что произвольная точка на прямой, соединяющей начало координат 0(0, 0, 0) с точкой М(x, y, 1), может быть задана тройкой чисел hx, hy, h (hx, hy, h) при h¹0. Вектор, определяемый тройкой чисел hx, hy, h, является направляющим вектором прямой, соединяющим точки 0 и M’. Эта прямая пересекает плоскость Z=h в точке (x, y, h), которая однозначно определяет точку x, y координатной плоскости XOY. То есть, между точкой x, y и множеством точек (hx, hy, h) h¹0 устанавливается

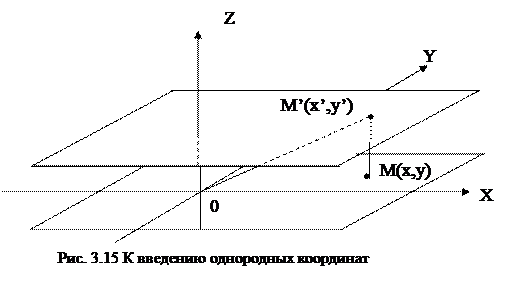взаимно однозначное соответствие, что и позволяет считать hx, hy, h ее координатами.

Однородное координатное воспроизведение неоднозначно, но равенство дополнительной координаты единице упрощает прямое и обратное преобразования и одновременно обеспечивает однозначность преобразований. Таким образом, описание точки на плоскости представляется вектором вида (x_i, y_i, 1) и однородные координаты можно представить как координаты двухмерной плоскости, рассматриваемой в трехмерном пространстве на уровне Z = 1. При помощи троек однородных координат можно описать любое аффинное преобразование на плоскости, то есть

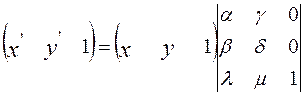
Элементы произвольной матрицы аффинного преобразования не несут явно выраженного геометрического смысла. Поэтому, чтобы найти то или иное отображение, используется соответствующее геометрическое описание, необходимые приемы, заключающиеся в последовательном использовании матриц поворота, масштабирования, отражения и переноса поэтапно, так как эти преобразования обладают хорошо выраженными геометрическими свойствами.

Пользовательская система координат (ПСК) отличается от мировой только тем, что мировая координатная система может быть только одна и положение ее фиксировано, она неподвижна.

Применение пользовательской системы координат практически не имеет никаких ограничений. Она может быть расположена в любой точке пространства под любым углом к мировой системе координат. Количество пользовательских систем координат не имеет ограничений, которые можно объявлять, сохранять и восстанавливать, поскольку проще выровнять систему координат с существующим объектом, чем определять точное положение трехмерной точки. ПСК обычно используют для работы с фрагментамирисунка, расположение которых заранее не может быть определено. ПСК используется для перемещения начала системы координат и/или изменения ориентации осей системы координат в пространстве, что значительно упрощает процесс создания и редактирования объектов. При создании объекта удобно поместить начало координатной системы объекта в опорную точку объекта, в особенности если в данной точке формируется много объектов. Из изложения понятно, что фрагмент создается в собственной ПСК и по мере готовности может быть промасштабирован, повернут и перенесен путем преобразования в мировую координатную систему. Поворот ПСК упрощает указание точек трехмерных или повернутых видах.

При работе ПСК пользователь может поворачивать ее плоскость (X,Y) и смещать начало координат. Все координаты при этом отсчитываются относительно текущей пользовательской системы координат. Пользовательская система координат по умолчанию совпадает с мировой.