Задания

В заданиях с №1 по №15 (таблица 3.1) необходимо вывести на экран таблицу значений функции Y(x) и ее разложения в ряд S(x) для х изменяющихся от 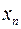до 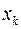с шагом 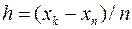. Близость значений S(x) и Y(x) во всем диапазоне значений x указывает на правильность вычисления S(х) и Y(x).

Таблица 3.1

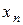
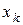
№			S(x)		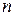Y(x)
	0.1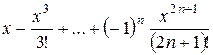
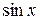
	0.1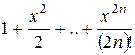
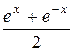
	0.1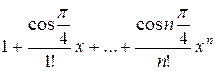
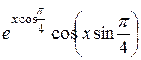
	0.1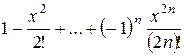
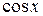
	0.1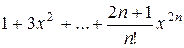
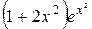
	0.1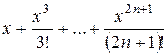
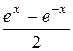
	0.1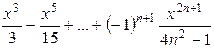
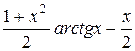
	0.1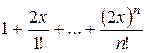
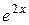
	0.1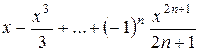
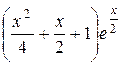
	0.1	0.5		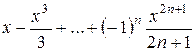	arctgx
	0.1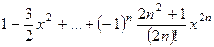
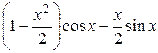
	0.1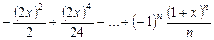
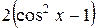
	-2	-0.1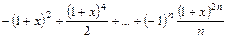
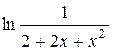
	0.2	0.8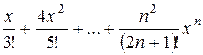
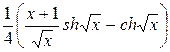
	0.1	0.8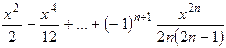

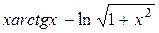
16. Посчитать k–количество цифр в десятичной записи целого неотрицательного числа n.

17. Переменной t присвоить значение 1 или 0 в зависимости от того, является ли натуральное число k степенью 3.

18. Дано n вещественных чисел. Вычислить разность между максимальным и минимальным из них.

19. Дана непустая последовательность различных натуральных чисел, за которой следует ноль. Определить порядковый номер наименьшего из них.

20. Даны целое n>0 и последовательность из n вещественных чисел, среди которых есть хотя бы одно отрицательное число. Найти величину наибольшего среди отрицательных чисел этой последовательности.

21. Дано n вещественных чисел. Определить, образуют ли они возрастающую последовательность.

22. Дана последовательность из n целых чисел. Определить, со скольких отрицательных чисел она начинается.

23. Определить k — количество трёхзначных натуральных чисел, сумма цифр которых равна n (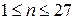). Операции деления (/, div, mod) не использовать.

24. Вывести на экран в возрастающем порядке все трёхзначные числа, в десятичной записи которых нет одинаковых цифр (операции деления не использовать).