Пусть 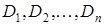 набор множеств, называемых областями значений (доменами), которым присвоены имена
набор множеств, называемых областями значений (доменами), которым присвоены имена 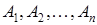 .
.
Определение 1. Пара 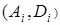 называется атрибутом с именем
называется атрибутом с именем 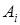 и областью значения
и областью значения 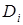 .
.
Обозначим через 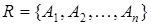 множество имен атрибутов, а через
множество имен атрибутов, а через 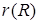 отношение
отношение 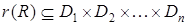 . Элементы отношения называются кортежами. Удобно представлять отношение как таблицу, где каждая строка есть кортеж и каждый столбец соответствует одному атрибуту, при этом порядок следования столбцов и строк не важен.
. Элементы отношения называются кортежами. Удобно представлять отношение как таблицу, где каждая строка есть кортеж и каждый столбец соответствует одному атрибуту, при этом порядок следования столбцов и строк не важен.
Определение 2. Конечное множество имен атрибутов 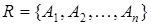 называется схемой отношения r(R).
называется схемой отношения r(R).
К отношениям применимы реляционные операции. Во-первых, это обычные булевы операции и, во-вторых, три специальные операции: выбора, проекции и соединения.
Если 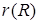 и
и 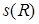 - отношения со схемой R, то
- отношения со схемой R, то 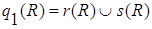 ,
, 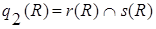 ,
, 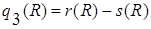 также являются отношениями со схемой R. При этом
также являются отношениями со схемой R. При этом 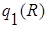 содержит все кортежи, которые принадлежат или r(R), или s(R);
содержит все кортежи, которые принадлежат или r(R), или s(R); 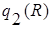 - все кортежи, которые принадлежат одновременно r(R) и s(R);
- все кортежи, которые принадлежат одновременно r(R) и s(R); 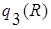 - те кортежи, которые принадлежат r(R), но не принадлежат s(R).
- те кортежи, которые принадлежат r(R), но не принадлежат s(R).
Определение 3. Операцией выбора (селекции) 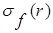 называется унарная операция, результатом применения которой к отношению r(R) является подмножество кортежей отношения r(R), удовлетворяющих условию выбора f
называется унарная операция, результатом применения которой к отношению r(R) является подмножество кортежей отношения r(R), удовлетворяющих условию выбора f
Очевидно, что 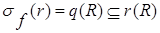 .
.
Определение 4. Проекцией отношения r(R) на множество 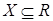 называется отношение
называется отношение 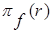 , полученное вычеркиванием столбцов в r(R), имеющих имена атрибутов из R-X, и удалением строк-дубликатов.
, полученное вычеркиванием столбцов в r(R), имеющих имена атрибутов из R-X, и удалением строк-дубликатов.
Очевидно, что 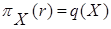 - отношение со схемой X и
- отношение со схемой X и 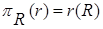 .
.
Определение 5. Соединением отношений r(R) и s(S), записываемым как 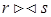 , называется отношение q(T), где
, называется отношение q(T), где 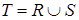 , каждый кортеж которого является комбинацией кортежа из r(R) и кортежа из s(S) с равными
, каждый кортеж которого является комбинацией кортежа из r(R) и кортежа из s(S) с равными 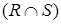 -значениями.
-значениями.
Если R=S, то 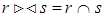 .
.
 2015-07-03
2015-07-03 307
307







