Методическое указание
К выполнению лабораторной работы №1
«Разложение периодических сигналов в ряд Фурье»
Йошкар-Ола
Теоретические сведения
Согласно теории Фурье функция 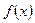 с периодом
с периодом 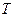 может быть разложена в тригонометрический ряд:
может быть разложена в тригонометрический ряд:
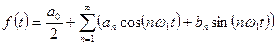 (1)
(1)
Где 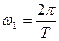 – основная частота.
– основная частота.
Коэффициенты a0, a1,... an и b1, b2,... bn, называемые коэффициентами Фурье, определяются выражениями
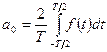
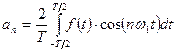
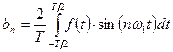 (2)
(2)
Для физических процессов протекающих во времени в качестве аргумента выступает время 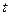 . Кроме того, сумма синусоидальной и косинусоидальной составляющих могут быть представлена в виде результирующих гармоник
. Кроме того, сумма синусоидальной и косинусоидальной составляющих могут быть представлена в виде результирующих гармоник
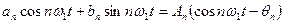 , (3)
, (3)
где 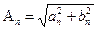 и
и 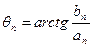 .
.
Таким образом функция 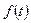 представляется в виде формулы
представляется в виде формулы
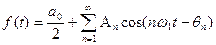 . (4)
. (4)
Совокупность гармонических составляющих, на которые раскладывается функция 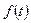 называется спектром сигнала (функции). Из формулы (4) следует, что спектр гармонической функции состоит из постоянной составляющей
называется спектром сигнала (функции). Из формулы (4) следует, что спектр гармонической функции состоит из постоянной составляющей 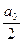 и множества гармоник, с частотами образующими дискретный ряд значений
и множества гармоник, с частотами образующими дискретный ряд значений 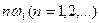 .
.
 2015-07-03
2015-07-03 311
311







