Методы доказательства неравенств
I. Доказательство неравенств с помощью определения
· 1. Неравенство Коши: 
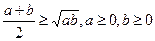
· 2. 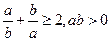
· 3. 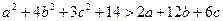
· 4. 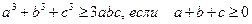
II. Синтетический метод доказательства
· 5. 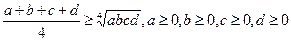
· 6. 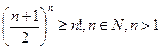
· 7. 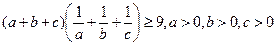
· 8. 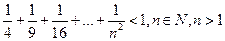
Упражнения
I.1) 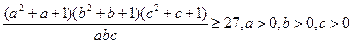
I.2) 8abc≤(a+b)(b+c)(c+a), a>0, b>0, c>0
I.3) 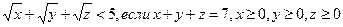
I.4) 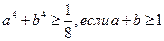
I.5) (x-3y)2+10(x-3y)+26>0 при любых x, y
I.6) 4xy+24x-10y-5x2-y2-30<0 при любых x, y
I.7) b2x2+(b2+c2-a2)x+c2>0> где a,b,c – длины сторон треугольника, х – любое
I.8) 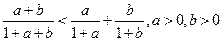
I.9) Доказать, что x+y≥2a если 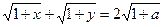
I.10) 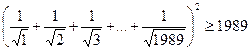
I.11) 
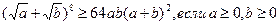
III. Метод «от противного»
· 9. 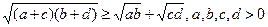
· 10. 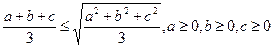
IV. Метод математической индукции
· 11. Доказать: 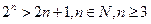
· 12. 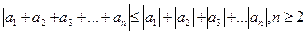
Упражнения
III.1) 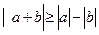
III.2) Если x>-1, n≥2, то (1+x)n≥1+nx
III.3) Если, n≥5, то 2n>n2
III.4) Если n≥2, то 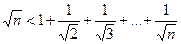
III.5) Если n≥2, то 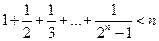
III.6) Если n 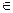 N, то
N, то 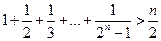
V. Метод производной
· 13. ex-x>1 при x≠0
· 14. cos x>1- 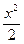 . x≠0
. x≠0
· 15. 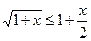 при x≥0
при x≥0
· 16. ln2n > ln (n-1)∙ln(n+1), n>2
Упражнения
V.1) 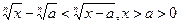
V.2) 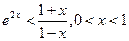
V.3) 2x4-4x3+3x2+4x+1>0, x>0
V.4) 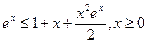
V.5) 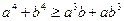
V.6) 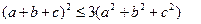
V.7) 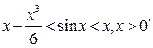
V.8) 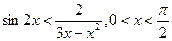
V.9) 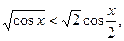
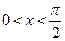
Дополнительный набор задач по всем методам
VI.1) 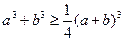
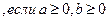
VI.2) 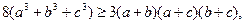
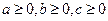
VI.3) 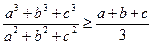 ,
, 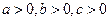
VI.4) 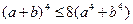
VI.6) 
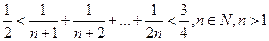
VI.7) 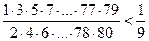
VI.8) 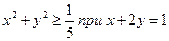
VI.9) 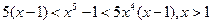
VI.10) 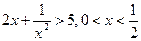
VI.11) ex>ex, x>1
VI.13) 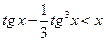 ,
, 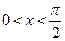
VI.14) 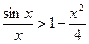 ,
, 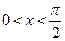
 2015-07-02
2015-07-02 406
406






