ТЕМА 5. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ДИСКРЕТНЫХ
СЛУЧАЙНЫХ ВЕЛИЧИН,
СВЯЗАННЫЕ С ПОВТОРНЫМИ ИСПЫТАНИЯМИ
ПЛАН
| 1. | Схема повторных испытаний |
| 2. | Формула Бернулли. Биномиальные вероятности |
| 3. | Биномиальный закон распределения |
| 4. | Математическое ожидание, дисперсия и график биномиального распределения |
| 5. | Распределение Пуассона |
| 6. | Гипергеометрическое распределение |
Пример 1. Монета подбрасывается 4 раза, пусть X - означает число появившихся гербов.
Пример 2. Известно, что в определенном городе 30% горожан предпочитают добираться на работу личным автомобилем. Случайно выбраны 8 человек. Пусть Y - число людей в выборке, предпочитающих личный транспорт.
Пример 3. Известно, что 15% деталей, произведенных автоматом, - бракованные. В порядке случайного отбора взято 12 деталей. Пусть Z - число дефектных деталей.
Что характерно для случайных величин X, Y и Z?
Это – примеры ДСВ, подчиняющихся вероятностному закону распределения, известному как биномиальное распределение.
Испытания Бернулли - это последовательность n идентичных испытаний, удовлетворяющих следующим условиям:
1. Каждое испытание имеет два исхода, называемые успех и неуспех. Эти два исхода - взаимно несовместные и противоположные события.
2. Вероятность успеха, обозначаемая p, остается постоянной от испытания к испытанию. Вероятность неуспеха обозначается q, где q=1 - p. Все n испытаний - независимы. То есть вероятность наступления события в любом из испытаний не зависит от результатов других испытаний.
Случайная величина, для которой вычисляется число успехов в n повторных испытаниях, где p - вероятность успеха в любом из заданных испытаний, а q = (1 - p) - соответствующая вероятность неуспеха, подчиняется закону биномиального распределения с параметрами n и p.
Пример 1. Монета подбрасывается 4 раза, пусть ДСВ X - означает число появившихся гербов.
При четырех подбрасываниях монеты случайная величина Х - число выпадений герба, принимает возможные значения Хi: 0,1,2,3,4.
Рассмотрим определенное событие, когда Х = 2. Событие состоит в том, что при 4-х подбрасываниях монеты 2 раза выпадет герб.
Определим вероятность этого события, то есть Р (Х =2). Подсчитаем, сколькими способами может осуществиться данное событие.
При 4-х бросаниях монеты герб появится два раза в одной из следующих 6 последовательностей:
ГГЦЦ, ГЦГЦ, ГЦЦГ, ЦГГЦ, ЦГЦГ, ЦЦГГ
Исходя из независимости 4-х испытаний, вероятность любой последовательности, скажем (Г, Г, Ц, Ц) есть ppqq. Очевидно, что порядок появления цифры или герба не влияет на вероятность. Вероятность p2q2 есть вероятность для любой из 6 перечисленных комбинаций.
Поскольку все шесть возможных комбинаций ведут к событию Х =2, то умножим результат на шесть, что даст нам 6p2q2. Для идеальной монеты p = q = 0,5; отсюда Р (Х =2) = 6∙(0,5)4 = 0,375.
Точно также можно вычислить другие вероятности Р(Х=0), Р(Х =1), Р(Х =3),Р(Х =4).
Обобщим процедуру вычисления вероятности появления некоторого события точно m раз в n последовательных испытаниях, удовлетворяющую условиям схемы повторных испытаний:
1.Вероятность любой заданной последовательности, в которой событие появляется m раз и в n испытаниях с вероятностью успеха в каждом отдельном испытании p и q - неуспеха, равна pmqn-m.
Для опыта с подбрасыванием монеты при p= q = 0,5, n = 4 и m = 2 получим
Р(Х=2) = (0,5)2(0,5)2 = (0,5)4
2. Число различных комбинаций в испытаниях, в результате которых наступит точно m успехов, равно числу сочетаний из n элементов по m элементов в каждом:
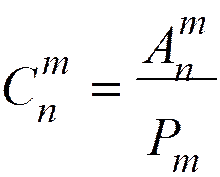 или
или 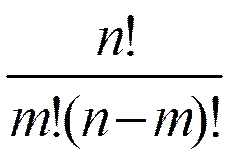
Для примера с подбрасыванием монеты
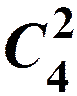 =
= 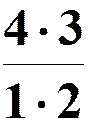 = 6 или
= 6 или 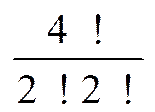
3.Поскольку существует С 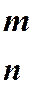 комбинаций и каждая комбинация имеет вероятность pmqn-m, то вероятность m успехов в n испытаниях есть результат двух описанных выше действий. Будем использовать символ Pn,m для обозначения вероятности Р(Х=m) в n испытаниях с вероятностью успеха в каждом отдельном испытании - p
комбинаций и каждая комбинация имеет вероятность pmqn-m, то вероятность m успехов в n испытаниях есть результат двух описанных выше действий. Будем использовать символ Pn,m для обозначения вероятности Р(Х=m) в n испытаниях с вероятностью успеха в каждом отдельном испытании - p
Р(Х=m) = Pn,m = С 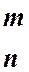 pmqn-m=
pmqn-m=
= 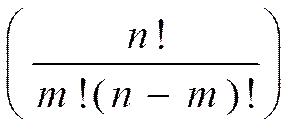 pmqn-m (1)
pmqn-m (1)
где p - вероятность успеха в отдельном испытании, q=1-p, n - число испытаний, m - число успешных испытаний.
Это -формула Бернулли.
В формуле (1) m может принимать значения от 0 до n. Подставим m=0,1,2,...,n в (1):
Построим биномиальное распределение числа выпадений герба при 4-х подбрасываниях монеты.
| X =m | P(x) = P4,m | ||
С 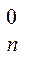 p0qn p0qn | 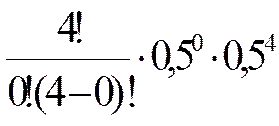 | 0,0625 | |
С 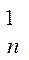 p1qn-1 p1qn-1 | 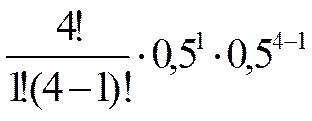 | 0,2500 | |
С 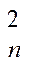 p2qn-2 p2qn-2 | 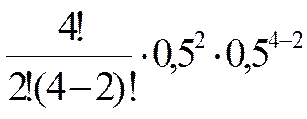 | 0,3750 | |
С 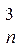 p3qn-3 p3qn-3 | 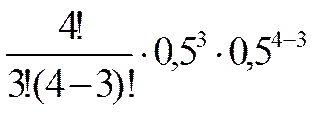 | 0,2500 | |
С 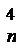 p4qn-4 p4qn-4 | 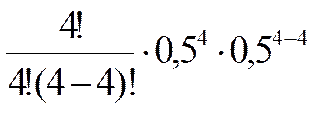 | 0,0625 |
Рассмотрим в качестве СВ Х число m наступления некоторого события в n независимых испытаниях. Очевидно, общее число появлений этого события в испытаниях состоит из суммы чисел появлений события в отдельных испытаниях, то есть Х=m=Х1+Х2+...+ +Хn, где Xi- число появлений события в i -том испытании (i=1,2,...,n).
Так как вероятность наступления события в каждом испытании постоянна и равна р (не наступления - q), то для каждой случайной величины Хi имеем распределение вероятностей:
xi 0 1
pi q p
Следовательно,
М(Х1) = М(Х2) =... = М(Хn)
M(Xi) = 0 ∙ q + 1 ∙ p = p
Исходя из формулы математического ожидания СВ, получим:
М(Х) = М(Х1) + М(Х2) +... + М(Хn) =
= 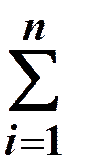 М(Хi) = np
М(Хi) = np
Математическое ожидание частоты биномиального распределения
М(Х) = np (2)
Аналогично рассуждая и применяя формулу дисперсии СВ получим:
D(Xi) = M(X2i) - M2(Xi) = 02 q + 12 p - p2 = p(1-p) = pq
D(X) = D(X1) + D(X2) +...+ D(Xn) = 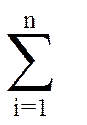 D(Xi) = =npq
D(Xi) = =npq
Дисперсия частоты биномиального распределения:
s2 = D(X) = npq (3)
Стандартное отклонение биномиального распределения:
s =√npq
Используя формулы (2) и (3), найдем математическое ожидание и дисперсию случайной величины Х - числа появления гербов при 4-х подбрасываниях монеты:
М(Х) =np = 4 ∙ 0,5 = 2.
Полученное значение интуитивно понятно и без вычислений. При достаточно большой серии испытаний по четыре подбрасывания монеты, мы ожидаем, что в среднем при четырех подбрасываниях монеты приходится два герба. Дисперсия Х есть
npq = 4 ∙ 0,5 ∙ 0,5 = 1,00.
| | 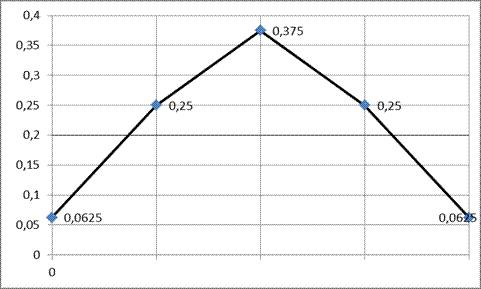 | |||||||||
Как видно из графика на рисунке 1 при m=2 вероятность достигает максимального значения. Частота m, равная 2, называется вероятнейшим числом или вероятнейшей частотой (наивероятнейшей).
Вероятнейшей частотой наступления события называется та частота, при которой вероятность достигает своего наибольшего значения и обозначается m0.
np - q£m0£np + p (5)
В этом неравенстве m0 может быть только целым числом.
Замечание: Если np - целое число, то m0 = np
Пример 2. Вероятность того, что выписанный продавцом чек будет оплачен, равна 0,9. Какое наивероятнейшее число чеков будет оплачено, если выписано 40 чеков?
Находим произведение np=40×0,9=36 (целое число), значит, m0=36
Найдем m0 по формуле (5)
40 ∙ 0,9 - 0,1 £m0 £40 ∙ 0,9 + 0,9
35,9 £m0£ 36,9
Какое целое число удовлетворяет этому двойному неравенству? m0 =36
Если вероятность появления события А в n отдельных независимых испытаниях очень мала
(p<q), то для вычисления вероятности применяется формула Пуассона:
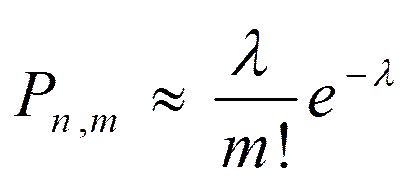 (6)
(6)
где l = np, n - число независимых испытаний с постоянной малой вероятностью р, е - основание натуральных логарифмов (е =2,71828), m - число появлений события (m i =0,1,2,3,...).
Для представления закона распределения Пуассона в виде ряда распределения придадим m целые неотрицательные значения m = 0,1,2,..., n и вычислим соответствующие им вероятности Pn,m:
Таблица 1.
Закон распределения Пуассона
| m | ... | k | ... | n | ||||
| Pn,m | e -l | l e -l | 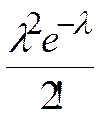 | 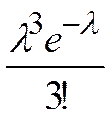 | ... | 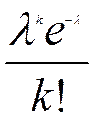 | ... | 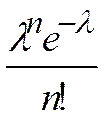 |
Сумма вероятностей ряда равна 1.
Закон распределения Пуассона можно записать также в виде функции распределения 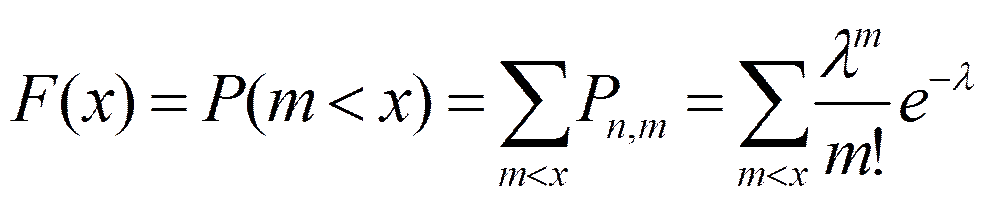 (7)
(7)
где знак 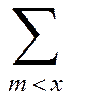 означает сумму вероятностей Pn,m для всех m, меньших n.
означает сумму вероятностей Pn,m для всех m, меньших n.
Поскольку вероятности Pn,m³1 и Pn,0 есть вероятности противоположных событий, то
Pn,m³1 = 1 - Pn,0 = 1 - 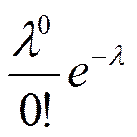 = 1 - е-l,
= 1 - е-l,
или
Pn,m³1 = 1 - е l (8)
Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона, совпадают и равны параметру l, который определяет этот закон, т.е.
М(Х) = D(Х) = l(9)
Пример 3. Нас интересует число инкассаторов, прибывающих утром на автомобиле в банк в течение 15 минут. Если предположить, что вероятность прибытия автомобиля одинакова в любые два периода времени равной длины, и что прибытие или неприбытие автомобиля в любой период времени не зависит от прибытия или неприбытия в любой другой период времени, то последовательность прибытия инкассаторов в банк может быть описана распределением Пуассона.
РЕШЕНИЕ. Анализ предыдущих данных показал, что среднее число инкассаторов, прибывающих в 15-ти минутный период, равно 10, тогда при l=10 получаем: P(m)=lm e-l/ m! =
= 10m e-10/m!, при m=0,1,2,...
Если необходимо узнать вероятность прибытия пяти инкассаторов в течение 15 минут, то при m = 5 получим:
Р(5) = 105 е-10/5! = 0,0378.
 2015-07-03
2015-07-03 2600
2600