Энтропия в открытых системах

В силу второго начала термодинамики, энтропия 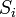замкнутой системы не может уменьшаться" (закон неубывания энтропии). Математически это можно записать так: 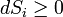, индекс 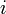обозначает так называемую внутреннюю энтропию, соответствующую замкнутой системе. В открытой системе возможны потоки тепла как из системы, так и внутрь неё. В случае наличия потока тепла в систему приходит количество тепла 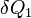при температуре 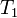и уходит количество тепла 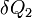при температуре 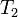. Приращение энтропии, связанное с данными тепловыми потоками, равно:

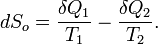
В стационарных системах обычно 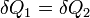, , 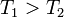так что 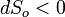. Поскольку здесь изменение энтропии отрицательно, то часто употребляют выражение «приток негэнтропии», вместо оттока энтропии из системы. Негэнтропия определяется таким образом как "отрицательная энтропия".

Суммарное изменение энтропии открытой системы будет равно:

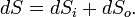
Если всё время 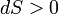, то рост внутренней энтропии не компенсируется притоком внешней негэнтропии, система движется к ближайшему состоянию равновесия. Если 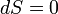, то мы имеем стационарный процесс с неизменной общей энтропией. В этом случае в системе осуществляется некоторая внутренняя работа с генерацией внутренней энтропии, которая преобразует, например, температуру 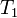внешнего потока тепла в температуру 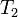уходящего из системы потока тепла.

В реальных экспериментах очень трудно измерить энтропию системы. Техники измерения базируются на термодинамическом определении энтропии и требуют экстремально аккуратной калориметрии.

Для упрощения мы будем исследовать механическую систему, термодинамические состояния которой будут определены через её объем V и давление P. Для измерения энтропии определенного состояния мы должны сперва измерить теплоёмкость при постоянных объёме и давлении (обозначенную C_V и C_P соответственно), для успешного набора состояний между первоначальным состоянием и требуемым. Тепловые ёмкости связаны с энтропией S и с температурой T согласно формуле:

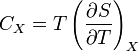
где нижний индекс X относится к постоянным объёму и давлению. Мы можем проинтегрировать для получения изменения энтропии:

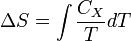
Таким образом, мы можем получить значение энтропии любого состояния (P, V) по отношению к первоначальному состоянию (P₀, V₀). Точная формула зависит от нашего выбора промежуточных состояний. Для примера, если первоначальное состояние имеет такое же давление, как и конечное состояние, то

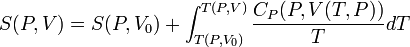
В добавление, если путь между первым и последним состояниями лежит сквозь любой фазовый переход первого рода, скрытая теплота, ассоциированная с переходом, должна также учитываться.

Энтропия первоначального состояния должна быть определена независимо. В идеальном варианте выбирается первоначальное состояние как состояние при экстремально высокой температуре, при которой система существует в виде газа. Энтропия в этом состоянии подобна энтропии классического идеального газа плюс взнос от молекулярных вращений и колебаний, которые могут быть определены спектроскопически.

Следующее уравнение может быть использовано для построения графика изменения энтропии на диаграмме P—V:

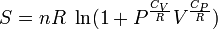
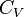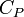Но предполагается, что и постоянные, что на самом деле не так.