Энтропия замкнутой системы не убывает (т. е. возрастает или остается постоянной)

Это утверждение также называют вторым началом термодинамики.

Второе начало термодинамики указывает направление процессов в изолированных системах. Самопроизвольные процессы в изолированных процессах идут в направлении увеличения энтропии. Если изолированная система находится в состоянии с максимальной энтропией, соответствующей ее энергии, то в ней не могут происходить никакие процессы, поскольку любой процесс привел бы к уменьшению энтропии. Таким образом, состояние с максимальной энтропией является наиболее устойчивым состоянием изолированной системы.

Рассмотрим некоторые примеры.

Теплопередача. Если привести в соприкосновение два тела А и В, температуры которых соответственно равны Т_A и T_B, то теплота будет переходить от более нагретого тела к менее нагретому, в результате чего температуры обоих тел будут выравниваться.

Пусть Та > T_B. Вычислим изменение энтропии, которым сопровождается этот необратимый процесс.

Состояние тела А изменяется при этом за счет потериим некоторого количества теплоты – δQ; соответственно тело В изменяет свое состояние за счет получения такого же количества теплоты δQ.

Для определения изменения энтропии системы, состоящей из обоих тел, нужно вычислить значения 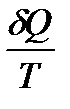= dS для какого-нибудь обратимого процесса, приводящего к тому же изменению состояния системы. Таким процессом может служить, например, процесс передачи тепла от тела А к телу В при помощи третьего рабочего тела, как это было сделано при рассмотрении процесса Карно, который, как известно, осуществляется обратимым путем на всех стадиях. Тогда для тела А и соответственно для тела В

.

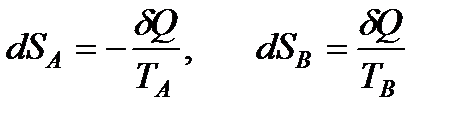Общее изменение энтропии обоих тел равно:

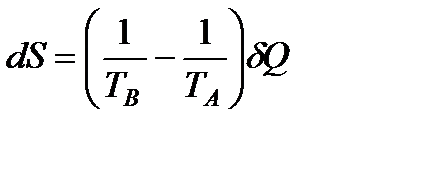
Поскольку Т_A > Т_B, то dS > 0, т. е. энтропия системы возрастает.

Приведенное рассуждение не зависит от того, посредством какого процесса осуществлен переход теплоты от тела А к телу В — теплопроводностью или излучением. Существенно лишь, что температуры обоих тел различны.

Изменение энтропии одного моля газа при изменении температуры и давления дается выражением:

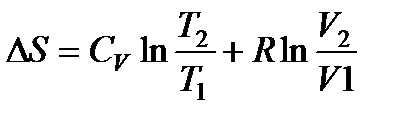, (145)

где T₁, T₂, V₁, V₂ – значения температуры и объема в начальном и конечном состояниях, R – газовая постоянная. Таким образом, энтропия возрастает как при увеличении температуры, так и при увеличении объема газа.

При адиабатическом расширении газа в пустоту работа не совершается и, следовательно, температура не изменяется. Однако, тем не менее, согласно формуле (145), энтропия газа повышается.

Рост энтропии при взаимной диффузии газов. Если привести в соприкосновение два различных газа, то они сами собой, без всякого внешнего воздействия, перемешаются благодаря взаимной диффузии. Обратный процесс, т. е. разделение газовой смеси на ее компоненты, сам собой не происходит и возможен только при определенном внешнем воздействии. Перемешивание газов — это необра­тимый процесс, и он должен поэтому сопровождаться ростом энтропии.

Действительно, представим себе, что в сосуде объемом V₁ находится 1 моль некоторого идеального газа. В другом сосуде объемом V₂ содержится 1 моль другого газа. Соединим вместе оба сосуда. Газы тогда смешаются и образовавшаяся смесь займет объем V = V₁ + V₂. Этот процесс можно рассматривать как расширение каждого из газов: первый расширился от объема V₁ до объема V, второй — от объема V₂ до объема V. При этом энтропия первого газа, согласно формуле (145), изменяется на величину 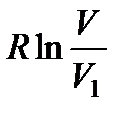, второго — на величину 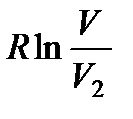. Общее же изменение энтропии ΔS выразится равенством

.

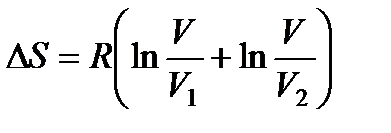Так как и V₁ и V₂ меньше; чем V, то ΔS > 0, т. е. энтропия системы возросла.