1. Зависимость энтропии от температуры. Третий закон термодинамики. Абсолютная и стандартная энтропия вещества.
2. Изменение энтропии – критерий направленности процесса. Изменение энтропии в различных процессах.
3. Термодинамические потенциалы. Полные и частные дифференциалы термодинамических потенциалов для закрытых систем. Критерии направления самопроизвольного процесса.
4. Уравнение Гиббса - Гельмгольца.
Из сказанного следует, что всякий самопроизвольный, следовательно, необратимый процесс в изолированной системе связан с увеличением энтропии. Равновесие характеризуется максимумом энтропии.
Таким образом, найден критерий возможности самопроизвольного протекания процесса, но только для изолированной системы.
Известно, что в изолированной системе нет только теплообмена с окружающей средой, но внутри нее могут идти процессы, сопровождающиеся перераспределением и превращением вещества и энергии. (Поэтому, рассматривая адиабатический процесс, в котором δQ=0 все равно нельзя считать, что ΔS =0.)
Если в объединенном уравнении первого и второго начала термодинамики вместо значения δQ подставить его выражение через теплоемкость, то получим:
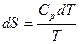
Интегрирование этого выражения от абсолютного нуля до температуры Т приводит к выражению:
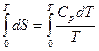
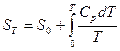
где S0 и S – энтропия вещества при абсолютом нуле и температуре Т соответственно.
Опытные данные показывают, что теплоемкости всех веществ при Т→0 резко падают до ничтожно малых величин, причем Ср уменьшается гораздо быстрее Т.
Определяя энтропии вещества при разных температурах, Нернст (1906) пришел к выводу, что изменение энтропии многих процессов, при температурах, близких к абсолютному нулю, пренебрежительно мало.
Позднее Планк (1912), Льюис и Рендал (1923) выдвинули постулат о том, что при абсолютном нуле энтропия S0 чистого кристаллического вещества без дефектов в кристаллической решетке равна 0. Этот постулат Планка настолько важный, что получил название третьего закона термодинамики:
При абсолютном нуле энтропия чистого кристаллического вещества без дефектов кристаллической решетки равна 0
или: Энтропия совершенного кристалла при 0 К равна нулю.
Энтропию, найденную относительно S0 = 0 называют абсолютной энтропией. Она, естественно, всегда положительна.
В расчетах всегда используют стандартную энтропию S0 298
Стандартной называют энтропию при стандартном давлении р = 1,013 Па и температуре Т (К). Для удобства сравнения и табулирования энтропии веществ относят к базисной температуре 298 К. Рассчитывают энтропию для 1 моль вещества при неизменном агрегатном состоянии по уравнению:
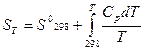
или 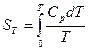
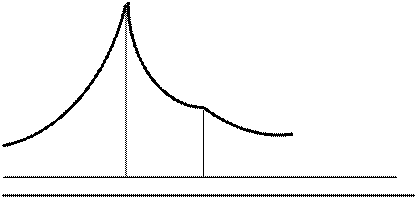
***Интеграл от ср тв/Т в пределах от 0 К до температуры плавления Тпл соответствует увеличению энтропии вещества в пределах области существования его в твердой области. Графически (рисунок 19) увеличение энтропии при нагревании вещество в твердом состоянии соответствует площади под кривой зависимости сртв/Т = f (T). При переходе в жидкое состояние при нормальной температуре плавления (Тпл) энтропия возрастает на энтропию плавления, равную энтальпии плавления (DHпл), деленной на Тпл в соответствии с уравнением (73). Нагреванию жидкости отвечает увеличение энтропии, вычисляемое по интегралу, в подынтегральную функцию которой входит теплоемкость жидкости (срж). Пределами интегрирования являются температура плавления (Тпл) и температура кипения (Ткип), т.е. область жидкого состояния. Из рисунка 19 видно, что увеличению энтропии при нагревании жидкости соответствует площадь под кривой зависимости срж/Т = f (T). Кипение жидкости при постоянном давлении и температуре кипения Ткип в соответствии с уравнением (73) соответствует возрастанию энтропии на энтропию кипения, равную энтальпии кипения (DHкип), деленной на Ткип. Нагревание газа до заданной температуры (Т) приводит к увеличению энтропии, которое рассчитывается по интегралу, в подынтегральную функцию которой входит теплоемкость жидкости (срж). Пределами интегрирования являются температура плавления (Ткип) и заданная температура (Т). Графически (рисунок 19) увеличению энтропии при нагревании жидкости соответствует площадь под кривой зависимости ср газ/Т = f (T).
Уравнение для вычисления абсолютной энтропии газообразного вещества будет иметь вид:
ST =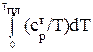 +
+ 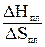 +
+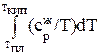 +
+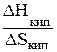 +
+ 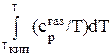 . (85)
. (85)
В таблицах стандартных величин приводятся данные 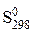 – значения энтропии при 298 К и нормальном давлении. Поэтому расчет изменения энтропии в результате протекания химической реакции проводят в два этапа: вначале по уравнению (86) находят DS 0298 по таблицам термодинамических величин, а затем по уравнению (87)- изменение энтропии от 0 К до Т:
– значения энтропии при 298 К и нормальном давлении. Поэтому расчет изменения энтропии в результате протекания химической реакции проводят в два этапа: вначале по уравнению (86) находят DS 0298 по таблицам термодинамических величин, а затем по уравнению (87)- изменение энтропии от 0 К до Т:
D 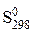 = SnJ
= SnJ 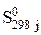 +Sn¡
+Sn¡ 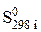 . (86)
. (86)
D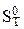 = D
= D 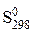 +
+  . (87)
. (87)

|
|
 | |||
|
0 Тпл Ткип Т, К
Рисунок 19 - Зависимость ср / Т от температуры
2. Изменение энтропии – критерий направленности процесса. Изменение энтропии в различных процессах. Изменение энтропии при фазовых превращениях.
В изолированной системе δQ=0, поэтому внутренняя энергия и объем постоянны. Тогда
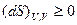
 и
и 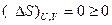
Отсюда следует, что в изолированной системе без сообщения энергии извне протекают только те самопроизвольные процессы, в которых энтропия растет. Процесс идет до тех пор, пока в системе не установится равновесие, характеризующееся максимальным значением энтропии:
S U,V =S max, (ΔS)u,v =0
Изменение энтропии при фазовых превращениях(изотермические процессы)
К фазовым превращениям относят процессы плавления, кристаллизации, испарения, конденсации и т.д. Такие процессы протекают при постоянном давлении и постоянной температуре. Изменение энтропии (S) в этих процессах можно вычислить по уравнению:
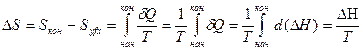
где ΔΗ и Т - молярная теплота и температура фазового превращения.
Знак изменения энтропии определяется знаком теплоты процесса, т.е. если ΔH>0, то и ΔS>0
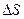 для обратимого изотермического расширения 1 моля идеального газа:
для обратимого изотермического расширения 1 моля идеального газа:
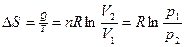
Изменение энтропии в химических реакциях. (При постоянном объеме)
При протекании химической реакции изменение энтропии рассчитывают с использованием значений стандартных энтропий ее участников:
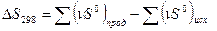
Нагревание вещества при постоянном давлении:
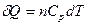
если в данном температурном интервале теплоемкость можно считать постоянной, то:
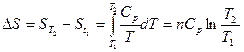
Термодинамические потенциалы. Полные и частные дифференциалы термодинамических потенциалов для закрытых систем. Критерии направления самопроизвольного процесса.
Энтропия является функцией, определяющей возможность протекания самопроизвольных процессов в изолированной системе.
Для закрытых систем аналогичными функциями являются термодинамические потенциалы: энергия Гельмгольца F (изохорно-изотермический) потенциал и энергия Гиббса G(изобарно-изотермический потенциал)/
В химии энергия Гиббса имеет более широкое применение при расчетах, так как химические реакции протекают чаще при постоянном давлении, а не при постоянном объеме.
Чтобы понять физический смысл энергии Гельмгольца, проинтегрируем при постоянных объеме и температуре объединенное уравнение 1 и 2 начал термодинамики:
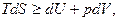

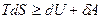
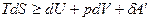
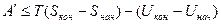
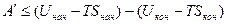
или
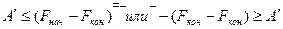
или
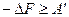 ,
,
(причем, знак равенства относится к обратимым, а знак неравенства – к необратимым процессам)
где 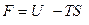
Это выражение показывает, что убыль энергии Гельмгольца характеризует работоспособность системы, т.е определяет ту часть энергии, которая в изохорно-изотермическом процессе превращается в работу. Ее также называют "свободной энергией".
Аналогично для изобарно-изотермического процесса получаем:
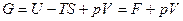
или
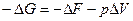 ,
, 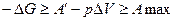
Убыль энергии Гиббса больше или равна максимальной полезной работе процесса А max.
Энергия Гиббса: 
Энергия Гиббса характеризует работоспособность системы, т.е. определяет ту часть энергии, которая в изобарно-изотермическом процессе превращается в работу. Энергия Гиббса называется свободной энтальпией.
Оба термодинамических потенциала являются функциями состояния системы, зависят от природы веществ участников реакции. их массы и температуры, т.е. являются экстенсивными свойствами системы.
Если продифференцировать функцию Гельмгольца 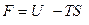 , получим выражение:
, получим выражение:
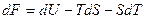 но
но
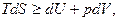 или
или
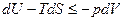
поэтому полный дифференциал функции Гельмгольца приобретает вид:
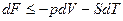
из этого следует, что энергия Гельмгольца зависит от параметров состояния V и Т.
А если так, то:

полный дифференциал дает возможность выяснить. как изменяется F при изменении параметров состояния..
Если Т= const, то dF= -pdV и поэтому
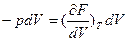 или
или

Если V = const, то из 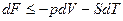 имеем
имеем
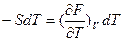 или
или  = -S
= -S
Эти равенства показывают, что при увеличении объема на единицу запас энергии Гельмгольца уменьшается на р единиц.
При увеличении температуры на единицу запас энергии Гельмгольца уменьшается на S единиц.
Это объясняется ростом хаотического движения молекул, уменьшающем работоспособность системы.
Дифференцируя функцию Гиббса 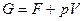
получим dG =dF+pdV+Vdp
подставляя значение F из 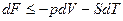
получим: 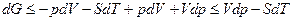
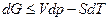 , то есть энергия Гиббса зависит от параметров p и T.
, то есть энергия Гиббса зависит от параметров p и T.
А если так, то полный ее дифференциал есть сумма:

Аналогично энергии Гельмгольца, для энергии Гиббса можно показать, что при T=const
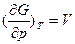
и при P=const
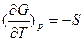
Это значит, что при увеличении давления в системе на единицу, энергия Гиббса увеличивается на V единиц.
При увеличении температуры на единицу энергия Гиббса уменьшается на S единиц.
Если процесс изохорно-изотермический, то уравнение полного дифференциала энергии Гельмгольца 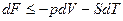
превращается в 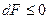
т.е. энергия Гельмгольца не изменяется в обратимом и убывает в необратимом процессах
Если процесс изобарно-изотермический, то уравнение полного дифференциала энергии Гиббса 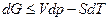
превращается в 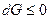
т.е. энергия Гиббса не изменяется в обратимом и убывает в необратимом процессах.
Отсюда следует, что по изменению величин термодинамических потенциалов можно судить о направлении самопроизвольных процессов.
Из изложенного следует вывод, что состояние равновесия характеризуется минимальным и постоянным значением термодинамических потенциалов.
Действительно, известно, что самопроизвольные процессы могут дать работу. равновесие наступает, когда эта возможность исчерпывается. Самопроизвольным процессам при постоянстве V и Т или Т и р соответствуют отрицательные изменения ΔF и ΔG. Чем ближе система к состоянию равновесия, тем меньше эти изменения. Если же они равны нулю, то система находится в состоянии равновесия.
Уравнение Гиббса - Гельмгольца.
Сочетанием уравнений 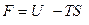 и
и  = -S и
= -S и
Гиббса 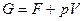 и
и 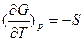
можно получить уравнения Гиббса-Гельмгольца:
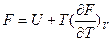 и
и 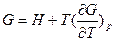
характеризующие запас свободной энергии для данного состояния системы в изотермических условиях.
На основе этих уравнений получают уравнения Гиббса-Гельмгольца для изменения термодинамических потенциалов:
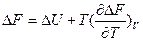 и
и 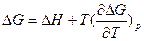 эти уравнения не используют в явном виде энтропию. Или:
эти уравнения не используют в явном виде энтропию. Или:
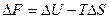 и
и 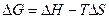
Эти уравнения наиболее применимы для расчета изменений функций Гельмгольца и Гиббса при протекании химических реакций. Они связывают максимально полезную работу, при переходе системы из состояния 1 в состояние 2 с тепловым эффектом перехода системы из состояния 1 в состояние 2.
Легко показать, что
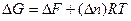
т.е. энергия Гиббса отличается от изменения энергии Гельмгольца на величину 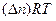
т.е. на изменение числа молей газообразных продуктов в ходе реакции.
Итак, если процесс идет при постоянном давлении и температуре и совершается полезная работа, то условием равновесия и самопроизвольности процесса будет
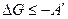
если при Р=const T=const работа полезная не совершается, то условием равновесия и самопроизвольности будет 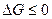
Пример 1.
Будет ли самопроизвольно идти образование паров воды из водорода и кислорода при температуре 110 С?
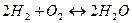 2Н2 + О2 =2 Н2О
2Н2 + О2 =2 Н2О
| S0298 | H2 O2 H 2O |
| Дж/моль*К | 0,13 0,2 0,19 |
стандартный тепловой эффект реакции равен ΔН0298=400 Дж/моль
Допустим, реакция идет при постоянном давлении, температура процесса постоянна по условию. Тогда критерием самопроизволности процесса является условие 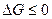
Используем уравнение Гиббса –Гельмгольца 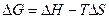
где ΔН – тепловой эффект процесса, TΔ S теплота, которая не может превратиться в работу, а ΔG – max полезная работа, взятая с обратным знаком.
тогда для стандартных условий имеем:
ΔН0298 =2 ΔН0298fН2Опар-(2 ΔН0298 f Н2+ ΔН0298 f О2)=400 Дж/моль
знак + показывает, что теплота поглощается.
изменение энтропии определяется на основании того, что энтропия является параметром состояния и в справочных данных даны не изменения энтропии, а абсолютные значения энтропий участников реакции:
ΔS0298 =ΣS0298 кон – ΣS0298 нач =2S0298Н2Опар-(2S0298 Н2+ S0298 О2)=2*0,19 – (2*0,13 +0,2)= - 0,1 Дж/мольK
так как температурный интервал реакции от25 до 110 < 100 C, изменением теплоемкости пренебрегаем и тогда
ΔНТ =ΔН0298 и -ΔST= ΔS0298
поэтому можем записать:
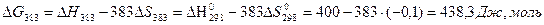 >0!!
>0!!
процесс самопроизвольно протекать не будет.
При V –const T=const можно воспользоваться уравнением
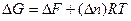
тогда 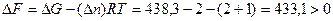
Вывод: так как в системе не совершается полезная работа, то при
V=const T=const и Р =const T=const самопроизвольно процесс протекать не будет.
Пример2. При какой температуре возможно самопроизвольное образование пара из Н 2 и О2?
Так как процесс идет при Р =const T=const, и не совершается полезная работа, то:
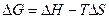 и
и 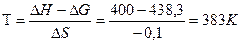
процесс пойдет самопроизвольно при температуре, >чем вычислена по уравнению т.е. при Т> 383К.
***
Расчет DG0Т по методу Темкина – Шварцмана. Изменение теплоемкости в результате протекания химической реакции в уравнении (97) выражается уравнением
Dср= Da + Db T+ DcT2 +Dc ¢ T-2. (98)
Проанализировав интегралы в уравнении (97) после подстановки в них уравнения (98), Темкин и Шварцман пришли к выводу, что их часть, связанная с температурой при эмпирических коэффициентах a, b, c, c ¢, может быть выражена общим уравнением:
Mn = 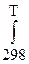 dT/T2
dT/T2 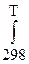 TndT, (99)
TndT, (99)
где n равно 0, 1, 2, -2 соответственно при Da, Db, Dc, Dc ¢.
Расчет в этом случае проводится по уравнению:
DG0 Т = DH0298 - ТDS0298 + DaМ0 + Db М1 +Dc М2 +Dc ¢ М-2 . (100)
Значения коэффициентов М0, М1, М2,М-2 приведены в таблицах термодинамических свойств.
3.25 Расчет DG0 Т с помощью функций приведенной энергии Гиббса. Под стандартным приведенным термодинамическим потенциалом (приведенной энергией Гиббса) понимают функцию:
Ф0T= - [G0 T – H00]/ T или Ф0¢T= - [G0 T – H0298]/ T, (101)
где G0 T – стандартное значение энергии Гиббса при температуре Т;
H00 и H0298 – стандартные значения энтальпии при 0 и 298 К, соответственно.
Из соотношения уравнения Гиббса
G0 T = H0Т - Т S0Т
и третьего закона термодинамики вытекает, что при Т=0 К G00 = H00 и уравнение (101) запишется так:
Ф0T = [H0Т - H00]/ T + S0Т . (102)
Расчет Ф0T проводятся по уравнениям
H0Т - H00 = 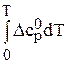 ,
,
S0Т = 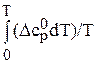 ,
,
откуда
Ф0T = - 1/Т 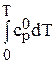 +
+ 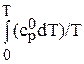 . (103)
. (103)
Так как вычисленные значения Ф0T для многих веществ приведены в справочниках, то расчет изменения энергии Гиббса в результате химической реакции можно провести по уравнению:
DG0 Т = -Т DФ0T + DH00, (104)
где D Ф0T – изменение приведенной энергии Гиббса химической реакции (вычисляемое по уравнению D Ф0T = ΣnJ Ф0T J - Σn i Ф0T i);
D H00 – стандартный тепловой эффект химической реакции при 0 К (который находят по закону Гесса).
Если в качестве базисной температуры выбрана не 0 К, а 298 К, то уравнение (104) примет вид:
DG0 Т = -Т DФ0¢T + D H0298, (105)
где DH0298 – тепловой эффект химической реакции, вычисляемый по теплотам образования или сгорания при температуре 298 К.
3.26 Зависимость энергии Гиббса от температуры и давления. Полный дифференциал от уравнения:
G = U + pv + TS
запишется так:
dG = dU + dpv +pdv + dTS + TdS. (106)
Подставив в уравнение (106) значение dU из объединенного уравнения первого и второго законов термодинамики:
dU = TdS – pdv,
получим:
dG = vdp - SdT. (107)
Поскольку G = f(T,p), то полный дифференциал от этой функции равен:
dG = ( G/
G/ Т) рdp + (
Т) рdp + ( G/
G/ р)Тdр. (108)
р)Тdр. (108)
Сравнение уравнений (107) и (108) показывает, что:
( G/
G/ Т)р = - S, (
Т)р = - S, ( DG/
DG/ Т)р = - DS,
Т)р = - DS,
( G/
G/ р)Т =v, (
р)Т =v, ( DG/
DG/ р)Т = Dv. (109)
р)Т = Dv. (109)
Аналогично можно определить зависимость энергии Гельмгольца от v и T:
dF = -pdv – SdT, (110)
( F/
F/ Т) v = - S, (
Т) v = - S, ( DF/
DF/ Т) v = - DS,
Т) v = - DS,
( F/
F/ v) T = - р, (
v) T = - р, ( DF/
DF/ v) T = - Dр. (111)
v) T = - Dр. (111)
При подставке в уравнения для энергии Гиббса и Гельмгольца
D F = DU - TDS,
DG = DH - TDS, (112)
значений DS из уравнений (109) и (111), получим уравнения для энергии Гельмгольца и Гиббса:
D F = DU + Т( DF/
DF/ Т) v,
Т) v,
DG = DH + Т( DG/
DG/ Т)р. (113)
Т)р. (113)
3.27 Зависимость энергии Гиббса от давления. Так как зависимость энергии Гиббса от давления выражается дифференциальным уравнением
( G/
G/ р)Т =v,
р)Т =v,
то
dG = vdp. (114)
Для идеального газа существует простое уравнение состояния - уравнение Менделеева – Клапейрона:
pv = RT,
по которому
v = RT/p.
Подставив последнее уравнение в (114), получим:
dG = RT dp/р = RTd lnр (115)
или
DG = RT 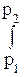 d lnр = RT ln(р2/р1). (116)
d lnр = RT ln(р2/р1). (116)
Уравнение (116) справедливо для идеальных газов, т.е. для газов при давлении до 10 относительных единиц давления (10.1,013.105 Па). Для реальных газов, чтобы не усложнять эту зависимость, Льюис (1901 г.) ввел понятие летучести или фугитивности - величины, которая вводится вместо давления для того, чтобы использовать уравнение состояния идеальных газов для реальных газов. Фугитивность или летучесть- это парциальная величина, характеризующая давление компонента смеси реальных газов fi, которая имеет размерность давления. При низких давлениях свойства реальной газовой смеси будут приближаться к свойствам идеального газа, а фугитивность fi* - к парциальному давлению р i* i – того компонента:
(fi)р®0 = fi* = р i*= х i Робщ, (117)
где х i – мольная доля;
Робщ – общее давление газовой смеси.
Соотношение
fi/ р i = fi/ х i Робщ = j i
называется коэффициентом фугитивности или летучести. Это безразмерная величина и в зависимости от условий может быть как меньше, так и больше единицы, а при малых давлениях равна единице:
lim fi/ р i = 1,
таким образом (j i)р®0 = 1 является условием нормирования фугитивности.
Уравнение для парциальной энергии Гиббса газовой смеси запишется так:
Gi = G0i + RT ln fif0i = G0i + RT ln 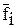 , (118)
, (118)
где 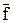 - относительная летучесть (также как и относительное давление выражается в относительных единицах давления, совпадающих с атмосферами).
- относительная летучесть (также как и относительное давление выражается в относительных единицах давления, совпадающих с атмосферами).
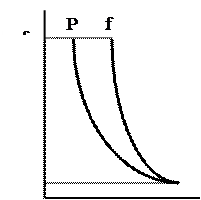
3.28 Графический расчет фугитивности. Графический расчет поясняется рисунком 20, на котором кривая АС описывает зависимость между давлением и объемом для реального, а кривая ВС - для идеального газа. В этом случае изменение энергии Гиббса для реального газа определяется уравнениями:
ΔG = RT ln p/p* = 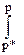 vdp,
vdp,
ΔG = RT ln f/f* =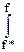 vdf.
vdf.
 | |||
| |||
A B
σ
P*, f* C
|
Из этого следует, что:
RT ln f/f* - RT ln p/p* = 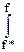 vdf -
vdf - 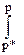 vdp = σ,
vdp = σ,
где σ – площадь между двумя кривыми.
Отсюда:
ln f/р = σ / RT. (119)
Уравнение (119) позволяет графически посчитать коэффициент фугитивности.
3.29 Аналитический расчет фугитивности. Используя различные уравнения состояния идеальных газов, можно применить соответствующие аналитические выражения расчета коэффициента фугитивности (σ):
- для уравнения Ван-дер-Ваальса
(p + a/v2) (v - b) = RT:
ln j =pv/z – a/(RTv) – ln[z – (1 – b/v)], z = pv(RT); (120)
- для уравнения Редлиха - Квонга
P =RT/(vb) – a/[ v(v+ b):
v(v+ b):
ln j = z – 1 – ln(z - b) – a/b ln(1 +b/z); (121)
- для уравнения Соава
P = RT/(v – b) – aα/[v(v + b)]:
ln j = z – 1 – ln[z(1- b/v)] - aα/(bRT) + ln(1 + b/v); (122)
- для уравнения Пенга – Робинсона
ln j = z-1-ln(z- b)-A/(2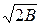 )ln(z + 2,414b)/(z- 0,414b). (123)
)ln(z + 2,414b)/(z- 0,414b). (123)
В уравнениях (120) – (123) a, b, α, A, B – эмпирические постоянные.
Уравнения (121) – (123) разработаны для углеводородов.
***
 2014-02-09
2014-02-09 11711
11711
