Политропный процесс

Политропным называется процесс, все состояния которого удовлетворяют условию:

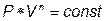, где n – показатель политропы, который может принимать любые значения - ∞.

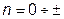Все выше рассматриваемые процессы являются частными случаями политропного процесса.

1. 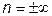- V=const – изохорный процесс (С_n=C_v);

2. 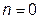- P=const – изобарный процесс (С_n=C_p);

3. 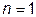- P 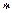V=const – изотермический процесс (С_n=∞);

4. 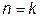- P 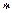V^k=const – адиабатный процесс(С_n=0)

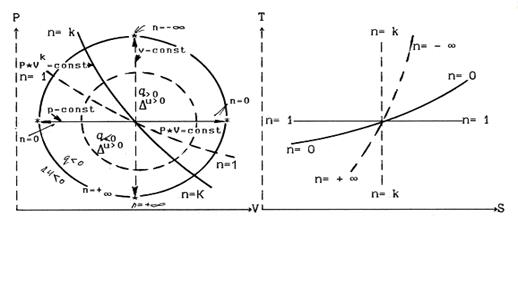
Так как уравнение политропного процесса имеет такой же вид, как и уравнение адиабатного, соотношение параметров для него будут аналогичны формулам для адиабатного процесса, в которых вместо показателя адиабаты (k) следует брать показатель политропы (n) (4.13)~(4.16).

Работу политропного процесса также рассчитывают по аналогичным формулам для адиабатного процесса(4.17)~(4.20).

Количество подведенной и отведенной теплоты можно определить с помощью Iго закона термодинамики:

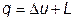, если

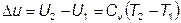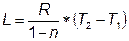; , то

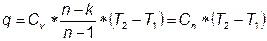, (4.21)

где С_n принимает следующие значения:

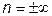С_n=C 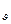; n=0 C_n=C_p; n=1 C_n=∞; n=k С_n=0.