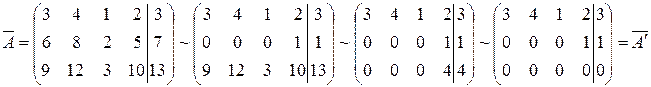
Матрица 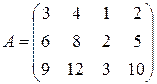 эквивалентна матрице
эквивалентна матрице 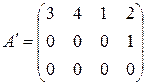 ранг которой равен 2, так как минор
ранг которой равен 2, так как минор 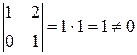 , а ненулевых миноров третьего порядка у данной матрицы уже не существует. Следовательно,
, а ненулевых миноров третьего порядка у данной матрицы уже не существует. Следовательно, 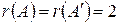 .
.
Матрица 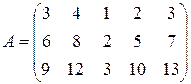 эквивалентна матрице
эквивалентна матрице 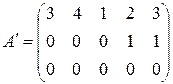 ранг которой равен 2, так как минор
ранг которой равен 2, так как минор 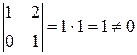 , а ненулевых миноров третьего порядка у данной матрицы уже не существует. Следовательно,
, а ненулевых миноров третьего порядка у данной матрицы уже не существует. Следовательно, 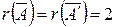 .
.
Так как 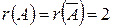 , то система (5) совместна.
, то система (5) совместна.
Для построения общего решения выпишем систему (6), соответствующую получившейся матрице 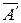 :
:
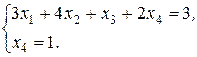 (6)
(6)
Заметим, что применяя метод подстановки (подставляя в первое уравнение системы (6) 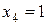 ), получаем:
), получаем:
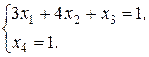 (7)
(7)
Из первого уравнения системы (7) следует, что одно из неизвестных выражается через две других. В данном случае, не имеет принципиального значения, какую из неизвестных мы оставим слева, а что перенесем вправо. Пусть слева остается 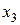 . Тогда
. Тогда
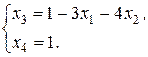 (8)
(8)
Этот выбор означает, что 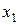 и
и 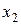 - свободные неизвестные, т.е. могут принимать любые действительные значения, а
- свободные неизвестные, т.е. могут принимать любые действительные значения, а 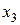 - базисная неизвестная.
- базисная неизвестная.
Общее решение в таком случае имеет вид:
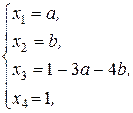 (9)
(9)
где 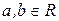 .
.
Если в качестве свободных неизвестных мы выберем 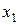 и
и 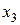 или
или 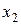 и
и 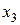 , то вид общего решения естественно изменится.
, то вид общего решения естественно изменится.
Замечание. Нетрудно заметить, что число свободных неизвестных в случае совместных систем всегда равно 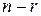 , где r – ранг матрицы из коэффициентов при неизвестных. Для построения решения в качестве базисных неизвестных выбирают неизвестные, коэффициенты при которых входят в один из базисных миноров. Оставляя их слева, остальные неизвестные переносят в правые части соответствующих уравнений. Вводя параметры для обозначения значений, которые принимают свободные неизвестные, получают систему, которую можно уже решить, используя ранее рассмотренные методы (правило Крамера или метод Гаусса). Более подробно эти вопросы будут рассмотрены на практических занятиях. Позднее, при изучении линейных преобразований, мы рассмотрим еще один метод построения общих решений линейных однородных систем.
, где r – ранг матрицы из коэффициентов при неизвестных. Для построения решения в качестве базисных неизвестных выбирают неизвестные, коэффициенты при которых входят в один из базисных миноров. Оставляя их слева, остальные неизвестные переносят в правые части соответствующих уравнений. Вводя параметры для обозначения значений, которые принимают свободные неизвестные, получают систему, которую можно уже решить, используя ранее рассмотренные методы (правило Крамера или метод Гаусса). Более подробно эти вопросы будут рассмотрены на практических занятиях. Позднее, при изучении линейных преобразований, мы рассмотрим еще один метод построения общих решений линейных однородных систем.
 2015-07-03
2015-07-03 556
556







