Закон Био–Савара–Лапласа: напряженность магнитного поля элемента тока длиной (dl), в вакууме, в точке отстоящей на расстоянии r, определяется соотношением: 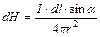 , где α – угол между направлением тока и направлением радиуса–вектора, проведенного к точке поля.
, где α – угол между направлением тока и направлением радиуса–вектора, проведенного к точке поля.
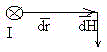
Рис. 2. К определению направления напряженности магнитного поля тока
Вектор напряженности направлен по нормали к плоскости, в которой лежат вектора dl и r, в соответствии с правилом правой руки: большой палец правой руки по току, тогда четыре укажут направление напряженности магнитного поля (на рисунке 2. ток течет от нас). Силовые линии магнитного поля прямолинейного проводника с током представляют собой концентрические окружности, расположенные в плоскости перпендикулярной току. Векторы напряженности поля направлены по касательным к силовым линиям в соответствии с правилом правой руки: большой палец по току, тогда четыре указывают направление обхода силовой линии.
Очевидно, что для вычисления полной напряженности магнитного поля, создаваемого в точке О током I, идущим по проводнику l, нужно геометрически суммировать элементарные напряженности dН, создаваемые всеми элементарными участками проводника dl и рассчитываемые по закону Био–Савара–Лапласа. Если проводник целиком расположен в одной плоскости, то напряженности от всех участков проводника имеют одинаковое направление, в этом случае геометрическое суммирование сводится к алгебраическому суммированию, то есть к интегрированию по всей длине проводника: 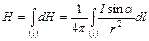 .
.
Примеры:
1. Напряженность магнитного поля конечного, прямолинейного проводника. Полная напряженность равна: 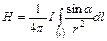 .
.
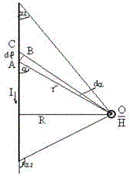
Рис.3. К расчету напряженность магнитного поля конечного, прямолинейного проводника
Выделим в проводнике элементарный участок dl на расстоянии r от точки О. Из точки О проведем радиусом r отрезок дуги 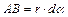 . Так как участок dl и угол dα малы, можно считать, что отрезок АВ прямолинейный, угол
. Так как участок dl и угол dα малы, можно считать, что отрезок АВ прямолинейный, угол 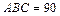 ° и угол
° и угол 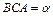 .
.
Тогда из ΔАВС получим r· 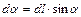 , откуда
, откуда 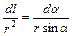 , учитывая, что
, учитывая, что 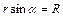 ,
, 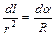 .
.
Введем последнее выражение в формулу для расчета напряженности, и перейдем от интегрирования по длине к интегрированию по углу: 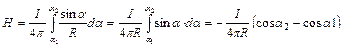 .
.
2. Напряженность магнитного поля бесконечного проводника с током. В случае бесконечного проводника 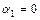 ° и
° и 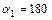 °. Подставив это в предыдущую формулу, получим:
°. Подставив это в предыдущую формулу, получим: 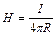 .
.
Примечание: на основании этого выражения дается определение единицы измерения напряженности магнитного поля – Ампер умножить на метр. Ампер на метр есть напряженность магнитного поля, создаваемого длинным прямолинейным проводником с током в 1А на расстоянии 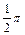 м от его оси.
м от его оси.
3. Напряженность магнитного поля в центре кругового тока. В этом случае 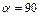 °, а I и
°, а I и 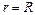 (где R – радиус кругового контура) имеют постоянные значения для всех участков dl. Поэтому
(где R – радиус кругового контура) имеют постоянные значения для всех участков dl. Поэтому 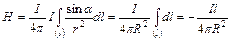 или, поскольку
или, поскольку 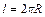 ,
, 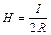 .
.
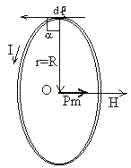
Рис. 4. К расчету напряженность магнитного поля в центре кругового тока
Очень полезное понятие магнитный момент кругового тока – это вектор расположенный перпендикулярно плоскости кругового тока в его центре и совпадающий по направлению с напряженностью, численно равен произведению силы кругового тока на обтекаемую им площадь: 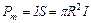 .
.
Круговой ток подобен постоянному магниту; во внешнем магнитном поле он ориентируется так, что его собственное поле совпадает с внешним. То есть, круговой ток поворачивается во внешнем магнитном поле так, что его магнитный момент устанавливается в направлении внешнего поля.
4. Напряженность магнитного поля на оси кругового тока. 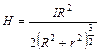 , где R – радиус кругового тока; r – расстояние вдоль оси до точки, в которой рассчитывается напряженность поля.
, где R – радиус кругового тока; r – расстояние вдоль оси до точки, в которой рассчитывается напряженность поля.
5. Напряженность магнитного поля соленоида. Соленоид – это катушка цилиндрической формы из проволоки, витки которой намотаны в одном направлении. 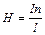 , где n – число витков на один метр длины соленоида; l - длина соленоида.
, где n – число витков на один метр длины соленоида; l - длина соленоида.
6. Напряженность магнитного поля тороида. Тороид – катушка из проволоки, навитой на тор. Магнитное поле тороида однородно и замкнуто внутри самого тороида. 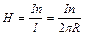 .
.
 2015-07-03
2015-07-03 2330
2330








