Методика изучения теоремы

Теорема: «Выделить из квадратного трехчлена 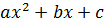квадрат двучлена значит записать его в виде 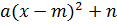, m, n- некоторые числа» вводится на уроке №11.

4.1. Подготовительный этап

4.1.1. Мотивация изучения теоремы

Квадратичной функцией называют функцию, которую можно задать формулой вида 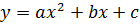, где 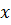- независимая переменная, а, 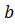, с- некоторые числа, причем а≠0.

Для мотивации необходимости изучения этой теоремы рассмотрим некоторую задачю.

1. Построить график функции .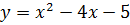

Приведем таблицу значений этого трехчлена при некоторых значениях х.

Х	-4	-2	-1
У				-5	-8	-9	-8	-5

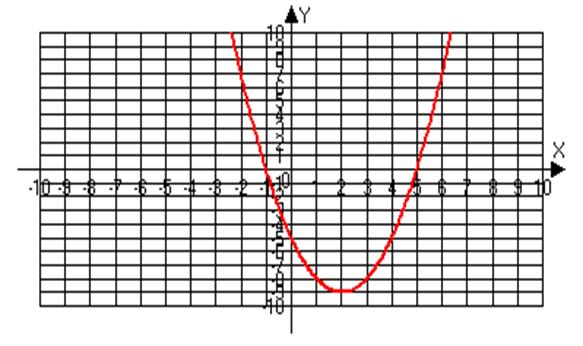
Рис. 16

Корнями трехчлена являются числа -1 и 5. Эти числа мы могли найти решив уравнение .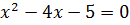

Рассматривая таблицу замечаем, что при увеличении значений х значения у сначала убывают, а затем возрастают.

4.1.2. Актуализация знаний и умений учащихся, необходимых для сознательного освоения теоремой

Для усвоения теоремы ученики должны владеть такими понятиями как:

· квадратичная функция;

· квадрат двучлена;

· график квадрата двучлена;

· преобразования графиков.

Упражнения на повторение этих понятий:

1. Какие из функций являются квадратичными?

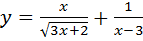
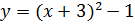
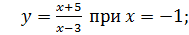
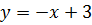
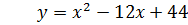
2. Укажите выражения, которые по вашему мнению, являются квадратом двучлена:

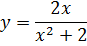
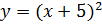
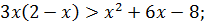
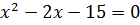
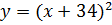
3. Постройте графики функций:

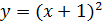
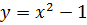
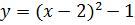
4. По построенным в задании 3 графикам, укажите геометрические преобразования, которыми вы пользовались в построении.

4.1.3. Подведение учащихся к формулировке

Для подведения учеников к теореме учитель предлагает классу построить графики некоторых функций.

1.

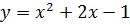
2.

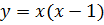
3.

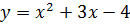
4.

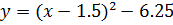
Для построения этих графиков можно пользоваться всем, что вы изучили ранее.

-Как вы будите строить график первой функции?

- Зададим функцию таблично.

- Да, в этом случае можно поступить так.

- Как построить график второй функции?

- Раскрыть скобки и задать функцию таблично.

-А что будем делать с функцией №3, как построить ее?

- Поступим аналогично, как с функцией №1.

- Как построить график функции №4?

- Можно использовать геометрические преобразования.

- Давайте построим графики функции №3 и №4, так как Вы предложили.

Построим график функции №3.

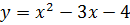
Х	-3	-2	-1
у				-4	-6	-6

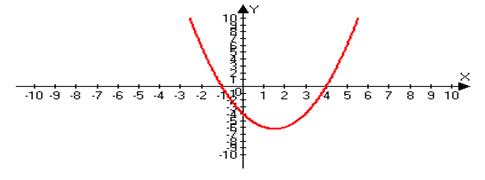
Рис. 17

Построим график функции №4

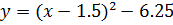
используя геометрические преобразования.

Построим график функции 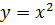, затем перенесем его на 1.5 вправо и опустим на 6.25 единиц вниз.

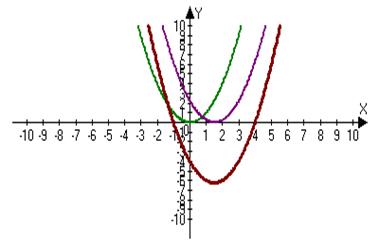
Рис. 18

Из построенных графиков функций видно, что графики получились одинаковые, но график функции №4 мы построили быстрее, используя геометрические преобразования.

Для более быстрого решения подобных задач применяют некоторую формулу:

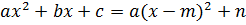, m, n- некоторые числа.

4.2. Основной этап

4.2.1.Формулировка теоремы, овладение содержанием, структурой и назначением

Запишем нашу теорему в импликативной форме:

«Если некоторый многочлен является квадратным трехчленом 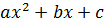, то его можно представить в виде 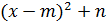, m, n- некоторые

числа».

В знаково- символьной форме теорема будет иметь вид:

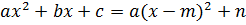
Запись на доске:

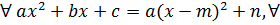m, n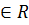

Теорема является простой, так как она содержит одно условие и одно заключение.

Эта теорема задает свойства квадратного трехчлена.

4.2.2. Формирование ориентировочной схемы доказательства

Теоремы

Поиск доказательства теоремы:

Учитель: Глядя на условие теоремы, как вы думаете, с чего необходимо начать ее доказательство?

Ученик: Мы знаем, что графиком этой функции является парабола, так давайте найдем координаты ее вершины.

Учитель: Да, правильно, мы должны" знать расположение данной параболы. А что еще видно из формулы которая находиться в правой и левой части равенства?

Ученик: Ну, если мы посмотрим на левую и правую части равенства, то увидим, что коэффициент а вынесен за скобки, в правой части.

Учитель: Молодец, точно подметил! Следовательно, при доказательстве данной теоремы, коэффициент а мы тоже вынесем за скобки. Посмотрим, что останется в скобках, которые мы видим должны быть полным квадратом, стоящим в правой части равенства.

Ученик: Значит, нам надо будет дополнить выражение в скобках так, чтобы получился полный квадрат!!!

Учитель: Ну, что же давайте запишем план доказательства и будем ему следовать.

План доказательства:

1. Запишем квадратичную функцию в общем виде у = .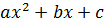

2. Находим вершину параболы.

3. В формуле квадратичной функции вынесем а за скобки, а 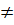0.

4. Дополним до удвоенного произведения.

5. Прибавим и вычтем .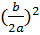

6. Сгруппируем до формулы.

7. Сравниваем левую и правую части равенства.

1.2.3. Проведение доказательства

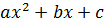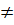Рассмотрим общий случай. Пусть имеется квадратичная функция у = , а 0.

Найдем вершину параболы.

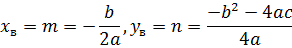
В 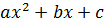вынесем а за скобки и дополним до удвоенного произведения, прибавим и вычтем .

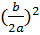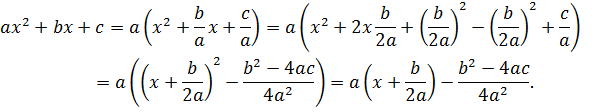
Заметим, что 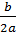= т, 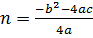запишем нашу формулу в этих обозначениях.

ах² + 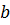х + с = а(х - т)² + п

Сравнив левую и правую части равенства, указанного в теореме мы видим, что теорема доказана.

4. 3.. Заключительный этап

4.3.1. Включение теоремы в систему знаний

Задача: Построить график квадратичной функции у = х² + 4x+3

Т.к. х² + 4х + 3 = х² + 4х + 4 — 4 + 3 = (х + 2)² — 1, то график такой функции можно получить из графика функции у = х² при помощи двух параллельных переносов: вдоль оси х на 2 единицы влево и вдоль оси у на 1 единицу вниз.

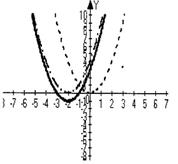
Рис. 19

Задачи для выполнения

Базовый уровень:

1. Найти координаты вершины параболы у = 2х² — 6х + 3. Пересекает ли эта парабола ось х?

2. Постройте графики функций:

у = х² + 2х — 3; у = -х² + 4х;

у = 2х² — 4х +3; у = -х² + 8х + 3

Достаточный уровень:

1. Постройте графики функций:

у = Зх² + 6х — 5;

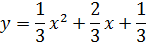
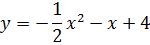
2. Постройте график функции у = х² + 6х + 5. Используя график, найдите:

-область значения функции;

-все значения х, при которых функция принимает отрицательные значения;

-промежуток, на котором функция убывает.

Высокий уровень:

Ø При каких значениях а и b вершиной данной параболы является данная точка А?

у = х² + + 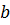х + с. А(-4;2)

Ø Постройте графики функций:

у = \2х² — 8х + 6|.

у = |-2х² + 8|х| - 6.