2015-07-04
903
Согласно формулам (1) и (9) получаем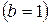 
:
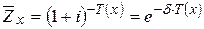, (10)
и нетто-премия будет равна математическому ожиданию
.
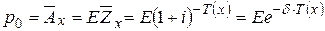Обозначив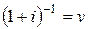 
, можем получить:
.
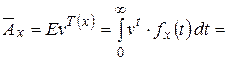
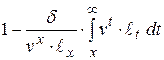А если ввести обозначение:
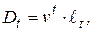(11)
то
.
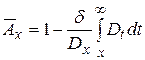Функцию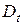 
называют замещающей или упрощающей, используется также и термин – коммутационная функция.
Для упрощения записи вводят и выражения:
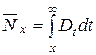, (12)
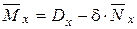, (13)
тогда
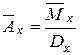. (14)
Величины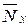 
и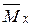 
также называются замещающими или упрощающими функциями. Они протабулированы в некоторых таблицах продолжительности жизни.
№ 7. Вычислите нетто-премию при заключении договора о полном страховании жизни человека в возрасте 30 лет, если предположить, что продолжительность жизни человека описывается моделью де Муавра с предельным возрастом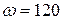 
лет, а эффективная годовая процентная ставка равна 
%.
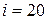Решение. Воспользуемся формулой:
.
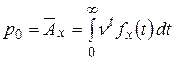Тогда, так как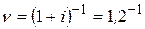 
и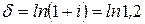 
, 
, 
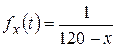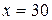, получаем:
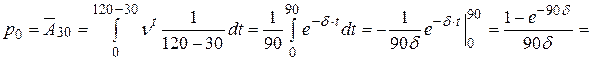
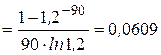(6,09 %).
Ответ: 6,09 %.
2.3. п -летнее чисто накопительное страхование жизни
Нетто-премия будет вычисляться как:
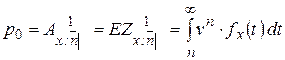
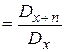. (15)
№ 8. Решите № 7 при условии заключения договора о трехлетнем чисто накопительном страховании.
|
|
|
Решение. Воспользуемся формулой:
.
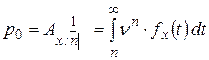Тогда, если продолжительность жизни описывается моделью де Муавра, получаем:
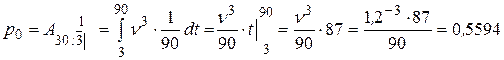(55,94%).
Ответ: 55,94%.
Если же в № 8 воспользоваться упрощающими функциями, то:
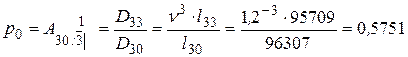(57,51%).
Видно, действительно, что аппроксимация законов продолжительности жизни моделью де Муавра несколько искажает результаты вычисления нетто-премий.
2.4. п -летнее временное страхование жизни
