Геометрическая интерпретация полностью интегрируемой системы

Рассмотрим систему с одной степенью свободы, совершающую финитное движение. Для таких систем фазовое пространство двумерно, а преобразование вида

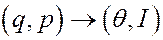(1)

осуществимо всегда. Для описания динамики удобна полярная система координат с 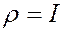и 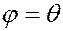. Тогда движение при заданном

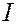будет происходить по окружности с радиусом .

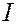Изменяя радиус, получим множество вложенных концентрических окружностей. Фазовое пространство разбито окружностями на совокупность колец. Скорость движения по индивидуальной окружности в общем случае зависит от : .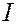

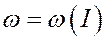Для системы с двумя степенями свободы фазовое пространство четырехмерно. Динамика таких систем: движение по окружности с центром 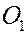, образованной переменными 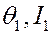и одновременно по окружности с центром 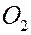(в плоскости, перпендикулярной плоскости окружности 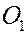), образованной переменными .

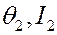Суперпозиция таких движений задает движение по поверхности тора, размерность которого равна двум.

Траектория, располагающаяся на торе, называется обмоткой тора.

Рассмотрим систему двух гармонических осцилляторов единичной массы, динамика которой в нормальных координатах описывается гамильтонианом

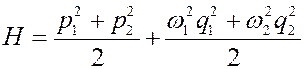. (2)

Фазовое пространство такой системы четырехмерно. Редуцированное пространство двухмерно. Проделаем каноническое преобразование по формулам, которые были получены ранее

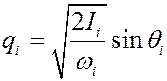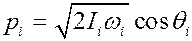, , (3)

.

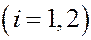Новый гамильтониан не зависит от переменных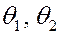

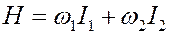. (4)

Поэтому

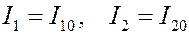. (5)

Далее

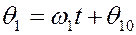, . (6)

В силу произвольности 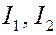все фазовое пространство оказывается расслоенным на совокупность вложенных друг в друга торов. Аналогичная картина будет иметь место для любой интегрируемой гамильтоновой системы с 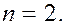Фазовые траектории будут располагаться на концентрических двухмерных торах.

При этом для нелинейных систем частоты обращения будут изменяться от тора к тору

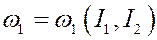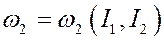, . (7)

Пусть

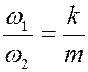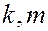, - целые числа. (8)

Зададим интервал времени

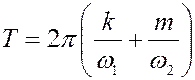. (9)

Тогда

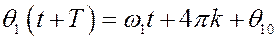, (10)

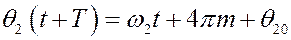. (11)

Поэтому через время 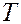траектория возвращается в точку, из которой она вышла в момент .

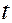Вывод: если частоты 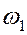и 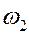соизмеримы, движение системы является периодическим с периодом 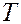и фазовая траектория представляет собой замкнутую непересекающуюся линию на торе.

При несоизмеримых частотах фазовая траектория образует всюду плотную обмотку тора. Такое движение называется квазипериодическим.

Пусть динамическая система является интегрируемой и 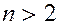. В этом случае фазовое пространство 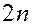- мерно и в переменных действие – угол имеет структуру множества определенных 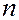- мерных торов, определяемых величинами 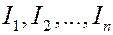и набором частот:

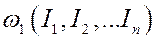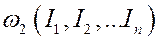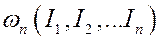, , …, . Любая траектория располагается на одном из них.

Опр. 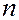- мерный тор называется резонансным, если выполняется соотношение

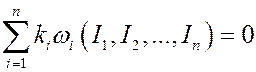. (12)