Оптимальное резервирование при ограничение веса аппаратуры

Оптимальное резервирование при ограничении веса аппаратуры

1. Оптимальное резервирование для получения требуемой величины вероятности отказа

Литература:

1. ГОСТ 27.002-89 Надежность в технике. Термины и определения.

2. Ничепоренко В.И. Структурный анализ и методы построения надежных систем, «Советское радио», Москва, 1968.

Севастополь

2010 г.

Оптимальное резервирование при ограничение веса аппаратуры

Резервирование позволяет из малонадежных элементов сконструировать достаточно надежную систему. Сравнительный анализ существующих методов и способов резервирования позволяет выбрать лучшие из них. Однако при этом увеличиваются вес, габариты и стоимость аппаратуры. Поэтому на практике возникает задача так зарезервировать систему, чтобы:

· ее вес, габариты и стоимость были бы не выше допустимых значений, а надежность максимальной (прямая задача);

· вероятность безотказной работы была не ниже требуемой, а вес, габариты и стоимость системы были бы минимальными (обратная задача).

Аналитическое решение этой задачи практически можно получить для случая поэлементного постоянного резервирования при одном ограничении. При нескольких ограничениях (больше 2) для интересующих практику случаев может быть построен алгоритм решения.

Более сложные случаи — резервирование замещением, учет надежности переключающих устройств, смешанное резервирование — до настоящего времени недостаточно исследованы. Однако и рассмотрение сравнительно простых случаев также может дать отправной материал для оценки возможностей и последствий реализации оптимального резерва.

Оптимальное резервирование при ограничении веса аппаратуры Пусть имеется нерезервированная система из п последовательных элементов; q₁, q₂, …,q_n — вероятности отказа этих элементов, a w₁, w₂,…,w_n — их веса.

Требуется произвести поэлементное резервирование этой системы так, чтобы вес ее не превышал заданного, а надежность была бы максимальной (вместо веса могут быть заданы габариты, стоимость).

Вес нерезервированной системы

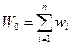(6.25)

Вероятность безотказной работы нерезервированной системы определяется выражением

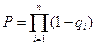(6.26)

Если каждый элемент системы зарезервирован (m_i-1) раз, то вес резервированной системы равен

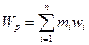, (6.27)

А вероятность ее безотказной работы

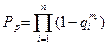(6.28)

Задача сводится к нахождению таких целых чисел m_i>1, при которых вероятность безотказной работы системы, определяемая из равенства (6.28), была бы максимальной, а вес ее не превышал допустимого W_доп^,

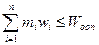(6.29)

Поставленная задача решена Ничипоренко В.И. [1], где утверждается, что на основании теории условного экстремума существует такое число λ, при котором в точке экстремума справедливо следующее равенство:

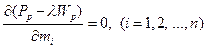(6.31)

Подставляя в равенство (6.31) вместо W_р и P_р их выражение из формул (6,27) и (6.28), получим

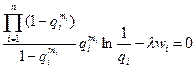
После преобразования: 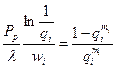(6.32)

Введя новые обозначения 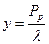, , 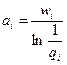равенство (6.32) можно переписать следующим образом: 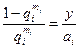(6,33)

Из этого уравнения получаем: 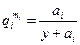, (6.34)

откуда после логарифмирования определяем 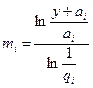(6.35)

Подставив это равенство в (6.30), получим:

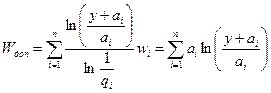(6.36)

Выражение (6.36) перепишем в виде 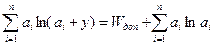(6.37)

Таким образом, для нахождения m_i, соответствующих точке экстремума функции P_p(m_i), необходимо найти y, удовлетворяющий уравнению (6.37). В [1] доказано, что существует единственный корень y₀>0 уравнения (6.37). Предположим, что этот корень y₀>0. Подставив его в формулу (6.35), определим m_i, соответствующие точке экстремума функции P_p(m_i)

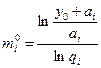(6.38)

Зная m_i⁰,определим максимальное значение вероятности P_p, которое может быть достигнуто для данного допустимого веса аппаратуры.

Подставляя 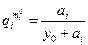в выражение (6.28), получаем

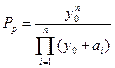(6.39)

Вычисленные по формуле (6.38) 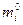могут иметь любые значения. Однако для практических целей необходимы целые значения 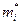дающие максимум функции P_p(m_i) и удовлетворяющие неравенству (6.29).

Среди целых чисел, отличающихся от 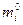не более чем на единицу, следует выбирать такие 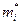, при которых по сравнению с другими возможными системами целых чисел удовлетворялись бы условия:

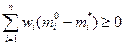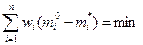; (6.40)

Если несколько {m_i} дают одинаковый минимум для

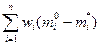, то среди них следует выбирать такую, которая удовлетворяет следующему условию: .

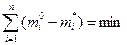Таким образом, зная вероятность отказа элементов q_i, составляющих систему, и их веса w_i, можно произвести поэлементное резервирование так, что вес резервированной системы не будет превышать допустимого, а вероятность безотказной работы будет максимальной.

Оптимальное резервирование для получения требуемой величины вероятности отказа.

Требуемую величину вероятности отказа не всегда удается получить только выбором высоконадежных элементов аппаратуры и наилучших схем. Для получения заданной надежности необходимо применять резервирование элементов аппаратуры. Однако возникает вопрос, как резервировать систему, чтобы требуемая величина вероятности была достигнута при минимальном весе (габаритах и стоимости) системы.

Пусть имеется нерезервированная система, состоящая из п последовательных элементов, которые имеют вероятности отказов q₁, q₂, …, q_n и веса w₁, w₂,…,w_n.Необходимо произвести поэлементное резервирование таким образом, чтобы вероятность исправной работы резервированной системы была больше требуемой или равна ей (P_р>= Р_тр) при минимальном ее весе.

Как видно, задача сводится к нахождению таких значений m_iпри которых требуемая величина вероятности исправной работы системы достигалась бы при минимальном ее весе.

Покажем, что формулы (6.38) и (6.39) справедливы и для этой задачи. Однако значение у₀ теперь необходимо находить не из формулы (6.37), а из (6.39).

Действительно, в данной задаче необходимо определить такие положительные целые числа m_i>=1, при которых бы выполнялось условие

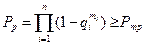, (6.41)

а вес системы 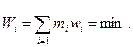(6,42)

В [1] показано, что точка (m₁⁰, m₂⁰, …, m_n⁰) с любыми (не только целыми) координатами, являющаяся решением поставленной задачи, удовлетворяет условию 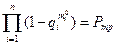(6.43)

и является точкой условного экстремума функции 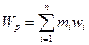при условии (6.43).

Очевидно, целочисленные значения m_i, доставляющие минимум функции W_p(m_i), при условии (6.43) следует искать среди целых чисел, отличающихся от m_i⁰ не более, чем на единицу.

На основании теории об условном экстремуме существует такое число σ, для которого в точке экстремума выполняется равенство

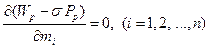(6.44)

Подставляя в данное равенство значения W_p и Р_р и дифференцируя по m_i получим

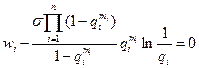(6.45)

Вводя обозначения 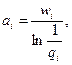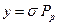и производя преобразования, получим 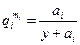(6.46)

Подставив выражение (6.46) в (6.43) получим

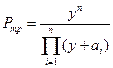(6.47)

В [1] показано, что существует единственное значение y₀, удовлетворяющее равенству (6.47).

Допустим, что значение корня y₀.> 0 найдено, тогда, подставляя его в формулу (6.46) и логарифмируя, получим

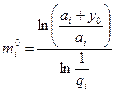(6.48)

Поскольку нас интересуют целочисленные значения m_i⁰ = m_i^*, то их нужно искать, исходя из критериев

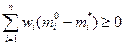
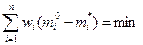
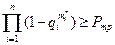(6.49)

Для нахождения y₀>= 0 из выражения (6.47) можно рекомендовать в качестве первого приближения взять у₀⁽¹⁾, вычисленный по формуле

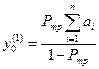(6.50)

Дальнейшее уточнение этого значения производится по методу Ньютона 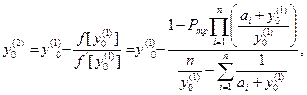(6.51)

где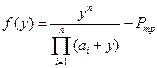

Для практических расчетов достаточно сделать одно - два уточнения.

Пример

Имеется нерезервированная система, состоящая из пяти элементов. Известны вероятности отказа в работе каждого элемента и их веса:

q₁= 0,2; q₂= 0,3; q₃= 0,4; q₄= 0,5; q₅= 0,6;

w₁=5 кг; w₂=3 кг; w₃=2 кг; w₄=4 кг; w₅=1 кг.

Требуется зарезервировать систему так, чтобы вес ее не превышал 60 кг, а вероятность ее исправной работы была бы максимальной.

Решение.

Вероятность безотказной работы нерезервированной системы определяется по формуле (6.26) и оказывается равной 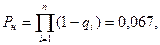то есть практически данная система мало пригодна для использования.

Вес нерезервированной системы согласно (6.25) равен

.

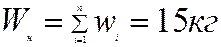1. Определяем значения:

;

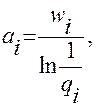
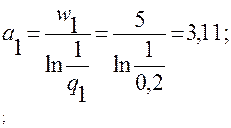
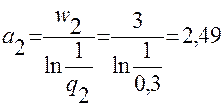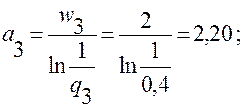
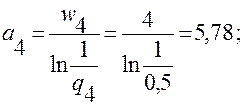
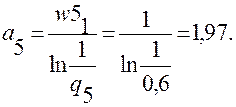
2. Используя вычисленные a_i, по формуле (6.37) определяем y₀:

3,11ln(y+3,11)+2,49ln(y+2,49)+2,2ln(y+2,2)+5,78ln(y+5.78)+1,97ln(y+1,97)= = 60 +3,11ln3,11+2,49ln2,49+2,2ln2,2+5,78ln5,78+1.97ln1,97

Решение этого уравнения является довольно трудоемкой задачей. Для нахождения первого приближения 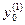принимаем значение, вычисленное по формуле 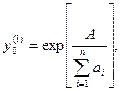(6.52)

где А – значение правой части уравнения (6.37).

Для данного примера А=79,27, поэтому

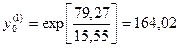
Используя метод Ньютона, уточняем первое приближение по формуле

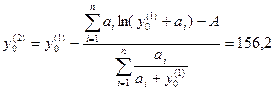
Путем линейной интерполяции этих двух значений получаем корень

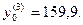
3. Пользуясь формулой (6.38), определяем

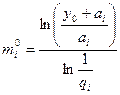
ИЗ вычислений видно:

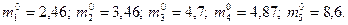
В данном примере рассмотрим три варианта для целочисленных значений 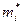(общее число вариантов – 32):

а – значения 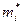, дробная часть которых меньше 0,5, округляем до целого в сторону уменьшения, а значения, дробная часть которых больше 0,5, округляем в сторону увеличения;

б – все значения 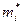округляем до целого в сторону уменьшения;

в - все значения 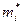округляем до целого в сторону увеличения;

Итак, имеем три варианта для целочисленных значений:

Вариант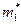
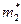
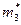
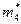
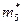
а
б
в

Вариант а

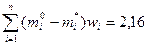
Вариант б

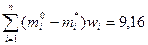
Вариант в

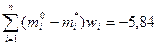
Согласно условиям (6.40) среди целочисленных значений следует выбирать такие, при которых, во - первых, 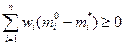, поэтому вариант в отпадает. Во – вторых, среди оставшихся вариантов необходимо выбрать такой, для которого .

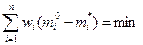В данном примере этому условию удовлетворяет вариант а

Приняв вариант а, можно получить лучшее приближение к 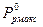по сравнению с каким – либо из двух других вариантов целочисленных значений .

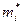4. Определим вероятность безотказной работы резервированной системы, для чего в формулу (6.28) подставим выбранные целочисленные значения :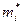

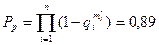
Максимальная вероятность безотказной работы системы, вычисленная по формуле (6.39), при дробных 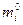равна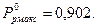

Итак, в результате решения поставленной задачи получена система, обладающая весом

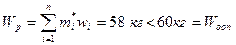и вероятностью исправной работы P_p=0,89.

Вывод: Тринадцатикратное увеличение вероятности безотказной работы системы достигается за счет четырехкратного увеличения ее веса.