На горизонтальной перекладине на тонких нитях подвешены три шарика с массами m, m1 и m соответственно. Шарики подвешены так, что два крайних соприкасаются со средним, а центры масс всех трех расположены на одной прямой. Левый крайний шарик отклоняют влево, поднимая на высоту h, затем отпускают. На какую максимальную высоту поднимется крайний правый шарик, если а) m1=m б) m1=2m? Все соударения считать абсолютно упругими. Какая из нитей и в какой момент времени будет иметь максимальное натяжение?
Решение:
1)
Пусть 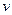 - скорость первого (отклоненного) шарика перед ударом,
- скорость первого (отклоненного) шарика перед ударом, 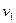 - скорость первого шарика после взаимодействия со вторым шариком,
- скорость первого шарика после взаимодействия со вторым шариком, 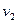 - скорость второго шарика после взаимодействия с первым,
- скорость второго шарика после взаимодействия с первым, 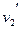 - скорость второго шарика после взаимодействия с третьим,
- скорость второго шарика после взаимодействия с третьим, 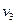 - скорость третьего шарика после взаимодействия со вторым.
- скорость третьего шарика после взаимодействия со вторым.
2)
Из закона сохранения для первого шарика имеем: 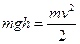
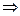
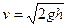 .
.
Считая, что после взаимодействия первый шарик отскакивает в обратную сторону, из закона сохранения импульса можно получить:
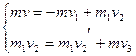
3)
Из закона сохранения энергии имеем:
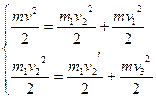
4)
Т.о. полная система уравнений из четырех неизвестных:
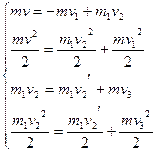 .
.
Ее решением является:
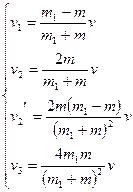
5)
Для случая 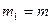 :
: 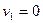 ,
, 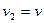 ,
, 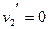 ,
, 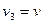
6)
Для случая 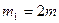 :
: 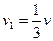 ,
, 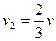 ,
, 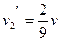 ,
, 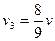
Ответ: а) 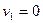 ,
, 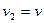 ,
, 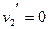 ,
, 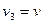 , б)
, б) 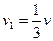 ,
, 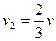 ,
, 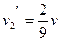 ,
, 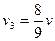
 2015-07-04
2015-07-04 272
272








