2015-07-04
533
Тонкостенный цилиндр, двигаясь без проскальзывания по горизонтальной плоскости, плавно переходящей в наклонную, закатывается на наклонную горку, на высоту 1м. Какой перепад высот преодолеет цилиндр, если на наклонной части «выключить» трение?
Решение:
1)
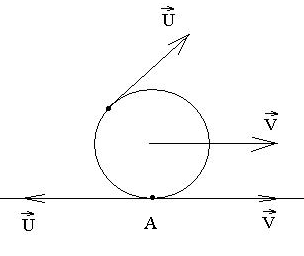
Случай с трением. Путь цилиндр двигается так, что его ось относительно плоскости имеет скорость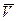 
, а нижняя точка цилиндра А (см. рисунок) в момент касания относительно плоскости не движется (нет проскальзывания).. Это может быть только в том случае, если 
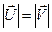, где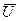 
- скорость точки А цилиндра относительно его оси. Перед горкой цилиндр массы 
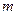обладает кинетической энергией 
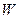, которая складывается из энергии поступательного движения 
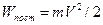, и энергии вращательного движения 
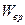. Энергия вращательного движения складывается из суммы энергий движения элементов тела относительно оси вращения. Поскольку вся масса тонкостенного цилиндра сосредоточена в ободе, скорость всех его элементов относительно одинакова: 
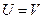. Поэтому энергия вращательного движения в данном случае определяется просто: 
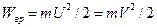. Соответственно полная кинетическая энергия цилиндра при движении по горизонтальной плоскости:
.
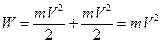Когда цилиндр остановится на горке, то он перестанет двигаться вдоль плоскости и вращаться, при этом вся кинетическая энергия перейдет в потенциальную энергию:
.
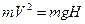В итоге, получаем: 
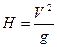
2)
Случай без трения. Если на наклонной плоскости трение «выключить», то при подъеме цилиндр будет продолжать вращаться с постоянной угловой скоростью, вплоть до самой верхней точки, и кинетическая энергия вращения в потенциальную энергию не перейдет. Высота подъема в этом случае определяется из соотношения: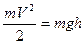 
. Соответственно, 
.
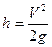3)
Сравнивая высоты из 1) и 2), получаем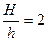 
.
Ответ: Если трение «выключить», высота подъема будет в два раза меньше, т.е. если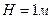 
, то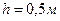 
. Сила трения «закатывает» цилиндр на наклонную плоскость.
