Закон Ома для участка цепи, содержащего источник э.д.с

(обобщенный закон Ома)

На рисунках 4а и 4б показаны одинаковые участки, содержащие последовательно включенные резистор Rи источник э.д.с. Е, по которым протекает токIодного и того же направления. Что касается источников, то э.д.с. в схеме на рисунке 4а совпадает с направлением тока, а на рисунке 4б – действует встречно с током.

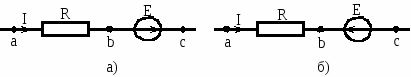
Рис. 4

К

(6)

ак известно, под напряжением U на участке цепи понимают разность электрических потенциаловφ между крайними точками этого участка (а и с на рисунке 4). Ток всегда течет от более высокого потенциала к более низкому потенциалу. Поскольку ток в обоих случаях (рис. 4а и 4б) направлен от точки а к точке с, то напряжение

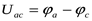
Выразим более высокий потенциал точки а через потенциал точки с. При перемещении (рис. 4а) от точки с к точке b (встречно к направлению э.д.с. Е) потенциал точки b оказывается ниже потенциала точки с на величину э.д.с. Е, то есть . Применительно к схеме на рисунке 4б потенциал точки b будет выше на величину э.д.с. Е, то есть 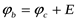. Поскольку потенциал точки а выше потенциала точки b на величину падения напряженияIRна резисторе с сопротивлениемR, то .

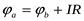Таким образом, для рисунка 4а: 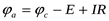, а для рисунка 4б: .

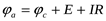Соответственно напряжение между границами а и с участка:

· д

(6а)

ля рисунка 4а:

;

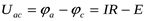· д

(6б)

ля рисунка 4б:

.

Решив равенства (6а) и (6б) относительно тока, получим обобщенный закон Ома (закон Ома для участка цепи, содержащего источник э.д.с.):

· д

(7а)

ля рисунка 4а:

;

· д

(7б)

ля рисунка 4б:

.

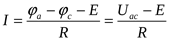В общем случае

(7)

В частном случае, когда э.д.с. отсутствует (Е = 0) уравнение (7) превращается в закон Ома для участка цепи, не содержащего э.д.с. (1).