Контрольная работа №1 по дисциплине «Математический анализ-2»-2012
ВАРИАНТ №0
| №п/п | Задания | Ответы |
| 1.1 | Неопределённый интеграл  равен равен 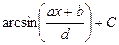 , где , где 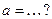 , , 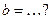  ( (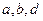 - целые числа). - целые числа).
| 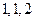
|
Ответ записать в виде: 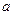 , , 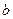 , , 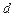
| ||
| 1.2 | Неопределённый интеграл  равен равен 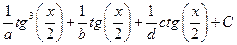 , где , где 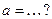 , , 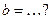  ( (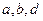 - целые числа). - целые числа).
| 
|
Ответ записать в виде: 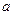 , , 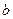 , , 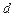
| ||
Неопределённый интеграл 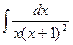 равен…. равен….
| 1) 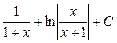
| |
1) 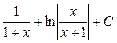 2) 2) 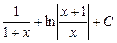 3) 3)  4)
4) 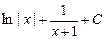 5) 5) 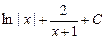
| ||
Определённый интеграл 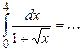
| 1) 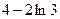
| |
1) 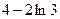 2) 2)  3) 3)  4) 4) 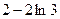 5) 5) 
| ||
Определённый интеграл 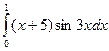 равен равен 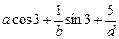 ,
где ,
где 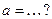 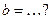  ( (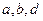 - целые числа) - целые числа)
| 
| |
Ответ записать в виде: 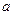 , , 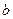 , , 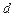
| ||
Площадь фигуры, ограниченной линиями 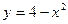 и и 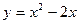 , равна… , равна…
| 2) 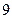
| |
1) 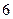 2) 2) 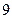 3) 3)  4) 4)  5) 5) 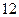
| ||
| 6.1 | Объём тела, полученного при вращении вокруг оси 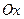 плоской фигуры, ограниченной линиями, плоской фигуры, ограниченной линиями, 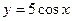 и и  на отрезке на отрезке 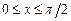 , равен , равен 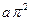 , где , где 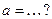 ( (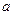 -целое число). -целое число).
| 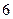
|
Ответ записать в виде: 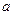
| ||
| 6.2 | Длина дуги кривой  на отрезке на отрезке 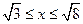 равна равна 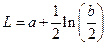 , где , где 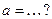 , , 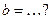 ( (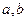 - целые числа). - целые числа).
| 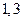
|
Ответ записать в виде: 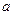 , , 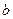
| ||
Функция 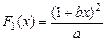 и и 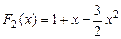 являются первообразными для одной и той же функции являются первообразными для одной и той же функции 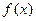 , если , если 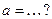 , , 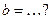 ( (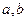 - целые числа). - целые числа).
| 
| |
Ответ записать в виде: 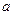 , , 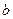
| ||
Несобственный интеграл 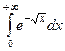 сходится, так как он равен конечному числу сходится, так как он равен конечному числу 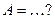 ( (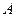 -целое число) -целое число)
| 
| |
Ответ записать в виде: 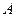
|
Примечание: В случае, когда ответ необходимо получить и результатом является нецелое число, то его следует записать в виде обыкновенной неправильной дроби, например: 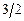 ,
, 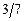 ,
,  .
.
Темы контрольной работы №1
 2015-07-04
2015-07-04 232
232







