Ранние и поздние сроки свершения событий. Резерв времени событий

Событие свершается в момент, когда предшествующие ему работы выполнены. Т.к. может быть несколько путей, предшествующих данному событию, то раннее время свершения события i – t 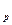(i) – определится продолжительностью максимального пути, предшествующего событию, т.е.

t 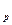(i)= t[L 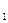(i)]. (1)

Cледовательно, чтобы найти раннее время свершения события, нужно знать критический путь ориентированного подграфа, состоящего из множества путей, предшествующих данному событию (1).

Как найти время позднего свершения события i: t 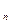(i)?

Каждое событие должно свершаться в такой срок, чтобы осталось достаточно времени для выполнения работ, следующих за этим событием.

Таким путем будет тот последующий, который имеет максимальную продолжительность L 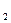(i). Самый поздний из допустимых сроков свершения события в сумме с продолжительностью выполнения последующих работ не должен превышать длины критического пути: t 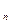(i)+ t[L 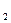(i)]= t 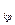. Отсюда:

t 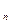(i) = t 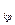- t[L 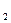(i)]. (2) т.е. поздний срок свершения события вычисляется как разность между продолжительностью критического пути и продолжительностью максимального из последующих за событием i путей (2).

Т.к. при вычислении критического пути методом динамического программирования у каждой вершины графа стоит максимальное время, необходимое для выполнения работ, следующих за этим событием, то расчет позднего времени свершения события не представляет труда.

Очевидно, для событий, лежащих на критическом пути, t 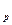(i)= t 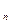(i).

Зная ранние и поздние сроки свершения событий сетевого графика, легко выяснить резерв времени каждого из них. Разница между наиболее поздним и наиболее ранним из возможных сроков называется резервом времени этого события, т.е.

R(i)= t 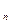(i)- t 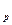(i) (3)

Резерв времени события i показывает максимальное допустимое время, на которое можно отодвинуть момент его свершения, не вызывая увеличение критического пути. События критического пути резерва времени не имеют.

Учитывая, что t[L 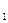(i)]+ t[L 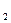(i)]=мах t[L(i)] - есть продолжительность пути максимальной длины, проходящего через событие, получим

R(i)= t 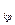- мах t[L(i)]= R 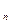[мах L(i)] (4)

Отсюда резерв времени любого события i равен полному резерву времени максимального пути, проходящего через это событие (4).

6.4 Графический метод расчета t 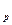(i), t (i) и R(i)

На практике получил широкое применение четырехсекторный способ расчета ранних и поздних сроков свершения события. При этом способе кружок сетевого графика, обозначающий событие, делится на 4 части (сектора) (см. рис.9).

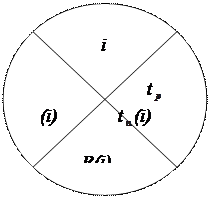
рис.9

Для получения применяют метод динамического программирования для расчета критического пути от нач.пути к завершающему. Чтобы получить t[L 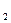(i)] для расчета t 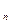(i)= t 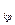- t[L 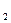(i)], берут тот же метод от завершающего события к начальному.