Решение

Построим сетевую модель и рассчитаем временные параметры событий (рис.11.8).

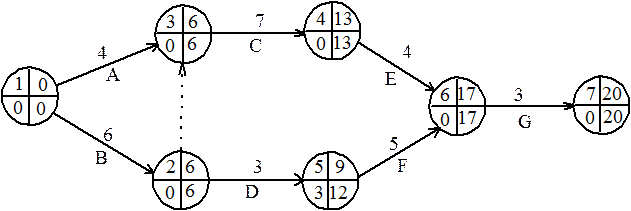
Рис.11.8. Сетевой график примера 2

Рассчитаем параметры сетевого графика

Код работы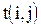
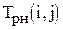
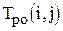
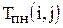
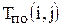
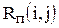
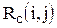
1,2
1,3
2,3
2,5
3,4
4,6
5,6
6,7

При поиске критических путей на сетевом графике будем использовать следующие условия его критичности:

· необходимое условие – нулевые резервы событий, лежащих на критическом пути;

· достаточное условие – нулевые полные резервы работ, лежащих на критическом пути.

Согласно необходимому условию два полных пути сетевой модели (см. рис.11.8) 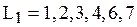и 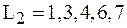могут быть критическими. Проверим достаточное условие критичности для работ (1,2) и (1,3)

;

.

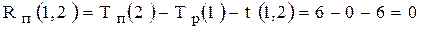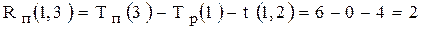Путь 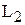, начинающийся с работы (1,3) не является критическим, т.к. как минимум одна из его работ (1,3) не является критической. Работа (1,3) имеет ненулевой полный резерв, а значит может быть задержана с выполнением, что недопустимо для критических работ.

Таким образом, сетевая модель имеет единственный критический путь 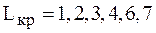длительностью 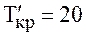недель. За выполнением работ этого пути необходим особый контроль, т.к. любое увеличение их длительности нарушит срок выполнения проекта в целом.

Работа D или (2,5) не является критической, ее полный резерв равен 3-м неделям. Это означает, что при задержке работы в пределах 3-х недель срок выполнения проекта не будет нарушен. Поэтому если согласно условию работа D задержится на 4 недели, то весь проект закончится на 1 неделю позже.