Растяжение, сжатие

ПОСТРОЕНИЕ ЭПЮР

Если брус без заделки (самоуравновешенный брус), то надо проверить его равновесие – алгебраическая сумма всех внешних сил, действующих на брус, должна равняться нулю.

Применяем метод сечений по участкам. Изображаем отрезанную часть бруса от свободного конца до разреза. Т. е. в отрезанной части не должно быть двух сечений, в ней не может присутствовать заделка.

В сечении прикладываем положительну ю осевую силу. Это растягивающая сила, ее вектор идет от сечения.

Записываем уравнение равновесия отрезанной части бруса. Это алгебраическая сумма всех сил на горизонтальную ось (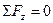). Получим выражение для осевой силы N, строим график, т. е. эпюру.

Особенности эпюр N, σ, w

На эпюре осевых силN

1. Под сосредоточенной силой - скачок на величину силы.
2. На участке с распределенной нагрузкой эпюра N это наклонная линия. Если распределенной нагрузки нет, то на этом участке эпюра N параллельна горизонтальной оси, т. е. N постоянна.
3. Если к концу бруса не приложена сила, то эпюра N начинается с 0, если сила приложена, то эпюра начинается с ординаты, равной этой силе: если сила растягивающая, то ординату откладываем вверх, если сжимающая, то вниз.

На эпюре нормальных напряжений σ

Эта эпюра подобна эпюре N, только появляется дополнительный скачок в месте резкого изменения площади сечения. Эпюра на участке с распределенной нагрузкой пересекает ось там, где будет экстремум на эпюре w.

На эпюре осевых перемещенийw

1. Эпюра w должна быть без разрывов (исключение – брус с зазором).
2. На участке с распределенной нагрузкой эпюра w это кривая, которая имеет экстремум там, где 0 на эпюре σ.
3. Уклон эпюры w изменяется в сечениях, где меняется величина или знак σ, этот уклон пропорционален величине σ (если знак s не изменился, то каждое последующее значение перемещения прибавляется к предыдущему, если s меняет знак, то последующее перемещение отнимается).
4. Прямолинейный и криволинейный участки эпюры w сопрягаются плавно, если в этом месте нет скачка на эпюре σ. При наличии скачка будет излом в сопряжении участков,

т. к. эпюра σ это производная от эпюры w, а эпюра w – интеграл от эпюры σ

(в масштабе).