2015-07-21
677
Если в точке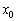
есть перегиб графика функции 
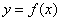, то:
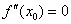либо значения 
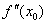не существует (разберём, читайте!).
Данная фраза подразумевает, что функция 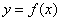непрерывна в точке 
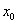и в случае 
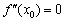– дважды дифференцируема в некоторой её окрестности.
Необходимость условия говорит о том, что обратное справедливо не всегда. То есть из равенства 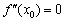(либо небытия значения 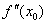) ещё не следует существования перегиба графика функции 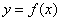в точке 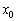. Но и в той, и в другой ситуации 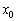называют критической точкой второй производной.
