Определим закон движения тела в среде, т.е. по какому закону будет изменяться глубина и скорость проникания.
Уравнения будем составлять при следующих допущениях:
- тело проникает в среду по нормали;
- движение прямолинейное с углом атаки, равным 0;
- тело в процессе проникания не деформируется.
В этом случае можно записать
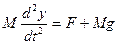 ,
,
где 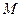 – масса тела,
– масса тела, 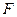 – сила сопротивления среды.
– сила сопротивления среды.
Или 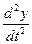 =
= 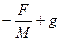
В нашем случае ускорением свободного падения можно пренебречь, т.к. 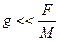
Выражение для силы сопротивления примем в виде двухчленной формулы
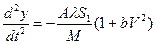
Начальные условия запишем в виде 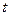 = 0,
= 0, 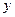 = 0,
= 0, 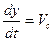 , где
, где 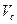 - скорость встречи.
- скорость встречи.
Будем составлять уравнение движения в параметрической форме
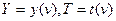
Тогда 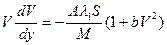
Проинтегрируем уравнение при указанных начальных условиях
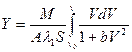
Введем новые переменную 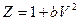 ,
, 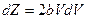
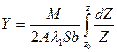
Обозначим 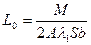 , тогда
, тогда 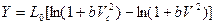
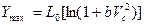 или, перейдя к десятичным логарифмам
или, перейдя к десятичным логарифмам 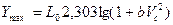
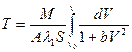
Введем новую переменную 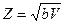 ,
, 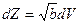
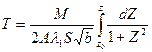
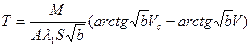
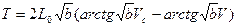
при 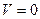
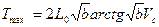
Коэффициенты 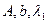 для расчета глубины и времени проникания приведены в табл. 13,14.
для расчета глубины и времени проникания приведены в табл. 13,14.
Таблица 13
| Среда | 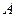 | 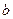 |
| Свеженасыпанная земля | 4,518´106 | 60´10-6 |
| Песок (грунт) | 4,263´106 | 20´10-6 |
| Глина | 10,251´106 | 35´10-6 |
| Дерево | 11,368´106 | 10´10-6 |
| Кирпичная кладка | 30,968´106 | 15´10-6 |
Таблица 14
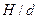 | 0…0,5 | 0,5…1,0 | 1,0…1,5 | 1,5…2,0 |
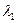 | 1,1 | 1,0 | 0,9 | 0,8 |
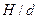 – удлинение головной части.
– удлинение головной части.
Представляет интерес зависимость скорости проникания от глубины проникания.

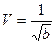
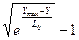
Для расчета взрывателей необходимо знать и зависимость силы сопротивления по пути и времени.
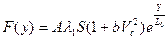
В конце проникания сила сопротивления становится равной силе статического сопротивления
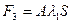
Все приведенные зависимости получены для условия, что поперечная площадь снаряда в процессе проникания постоянна. Однако это не так. Сила 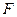 достигает максимума при
достигает максимума при 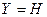 (длина головной части) и реальная зависимость
(длина головной части) и реальная зависимость 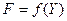 имеет вид (рис. 9).
имеет вид (рис. 9).




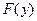 Теоретическая кривая
Теоретическая кривая
 |


 Экспериментальная кривая
Экспериментальная кривая
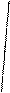 |


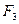

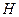
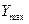
Рис. 9
Ввиду того, что 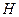 <<
<< 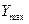 начальным участком можно пренебречь.
начальным участком можно пренебречь.
Рассмотрим подробнее характер влияния скорости встречи на полную глубину проникания.
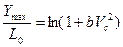
Очевидно, что при 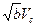 <<1
<<1
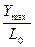 @
@ 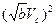
а при 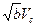 >>1
>>1
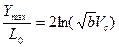
Таким образом глубина проникания 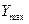 при малых скоростях встречи пропорциональна квадрату скорости встречи, а при больших – логарифму скорости встречи.
при малых скоростях встречи пропорциональна квадрату скорости встречи, а при больших – логарифму скорости встречи.
ln(1 + bV2c)




 Ymax K (Ö bVc)
Ymax K (Ö bVc)

 Lo
Lo

 (Ö b V2c)
(Ö b V2c)
 | |||
 | |||
 |
1 2ln(Ö b Vc)
 |

 0 1 2 3 Ö b Vc
0 1 2 3 Ö b Vc
Рис.10
Как следует из графиков с достаточной для практики точностью при 0,5 £ 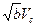 £ 3,5 зависимость может быть представлена прямой линией
£ 3,5 зависимость может быть представлена прямой линией
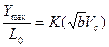
Подставляя в это уравнение значение 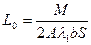
 и имея в виду, что
и имея в виду, что 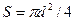 получим
получим 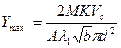 . Обозначим
. Обозначим 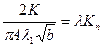 ,
,
тогда 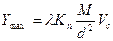
где 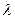 - коэффициент, зависящий от формы головной части,
- коэффициент, зависящий от формы головной части, 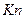 – коэффициент проникания, зависящий от свойств среды.
– коэффициент проникания, зависящий от свойств среды.
В таком виде формула была получена по результатам обработки экспериментальных стрельб, проведенных на острове Березань. Эта формула получила название “Березанской.”
Значения 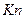 и
и 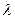 приведены в табл. 15, 16.
приведены в табл. 15, 16.
Таблица 15
| Среда | 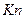 | Среда | 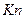 |
| Песок | 4,5´10-6 | Гранит | 1,6´10-6 |
| Глина | 7,0´10-6 | Сосна, ель | 5,0´10-6 |
 Известняк Известняк | 2,0´10-6 | Бетон высшего качества | 0,8´10-6 |
| Бетон среднего качества | 1,2´10-6 |
Таблица 16
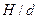 | 0…0,5 | 0,5…1,0 | 1,0…1,5 | 1,5…2,0 |
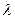 | 1,0 | 1,1 | 1,25 | 1,40 |
Пример: определить глубину и время проникания АБ ФАБ-500-М62.
Грунт – глина; 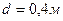 ;
; 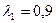 ;
; 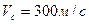
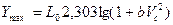
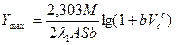
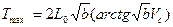
 2015-07-14
2015-07-14 1331
1331








