При взрыве заряда ВВ в воздухе сильно нагретые газообразные продукты детонации, имеющие начальное давление 104 Мпа быстро расширяются, сжимая окружающий воздух, образуя воздушную ударную волну, на фронте которой большое избыточное давление. При расширении продукты детонации совершают механическую работу и теряют радиальную скорость, вследствие чего воздушная ударная волна отрывается от них и распространяется в воздухе со сверхзвуковой скоростью. Объем, в котором поражающее действие производится продуктами детонации. Составляет 2000…4000 объемов приведенного заряда. Под приведенным зарядом понимается заряд ВВ сферической формы, но равной массы.
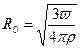
где w - масса заряда, r - плотность заряда.
Для правильного понимания вопросов, связанных с разлетом продуктов детонации и оценкой разрушающего действия взрыва, необходимо знать значения плотности, давления и скорости продуктов детонации, скорости звука в продуктах детонации за фронтом ударной волны.
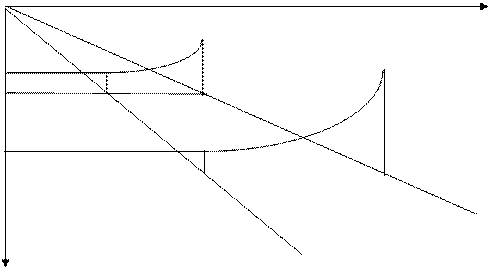
Рассмотрим простейший случай разлета продуктов детонации с открытой торцевой поверхности цилиндрического заряда в момент подхода к ней плоской детонационной волны (рис.19).
|
|
|
Допустим, что разлет продуктов детонации с боковой поверхности заряда и с его левого торца, на котором была возбуждена детонация, отсутствует.
D´t2
 |
D´t1
 | |||
 |
X
t1
t2 X = D´t

X = 0,5D´t

 Фронт детонационной волны
Фронт детонационной волны
 t Граница зоны покоя
t Граница зоны покоя
 |
Рис.19
В зоне покоя, занимающей объем от левого торца заряда 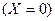 до половины длины пути, пройденного детонационной волной
до половины длины пути, пройденного детонационной волной 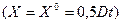 скорость движения продуктов детонации равна 0
скорость движения продуктов детонации равна 0 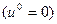 , а все параметры постоянны
, а все параметры постоянны 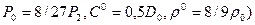 .
.
В зоне движения все параметры продуктов детонации возрастают к сечениям вблизи фронта детонационной волны 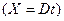 . При этом скорость продуктов взрыва u, скорость звука
. При этом скорость продуктов взрыва u, скорость звука 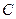 и плотность
и плотность 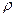 возрастают по линейному закону, а давление
возрастают по линейному закону, а давление 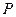 по закону кубической параболы (рис.20).
по закону кубической параболы (рис.20).
На фронте детонационной волны (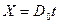 ) параметры продуктов взрыва достигают своих максимальных значений
) параметры продуктов взрыва достигают своих максимальных значений 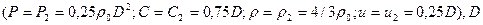 - скорость детонации.
- скорость детонации.





 1,4
1,4


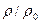
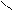
 1,2
1,2

 1,0
1,0

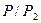

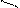
 0,8
0,8
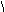


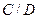
 0,6
0,6
 |

 0,4
0,4

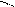

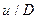
 0,2
0,2
 |
0 0,5 1 Х
 Dt
Dt
Рис.20
Итак, допустим, что плоская детонационная волна, распространяясь по заряду со скоростью 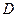 , дошла до открытого правого торца (сечение
, дошла до открытого правого торца (сечение
0 – 0 рис.21).
 |
 ВВВВ
ВВВВ
 |

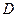



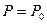

 Продукты детонации
Продукты детонации 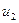
 | ||||
 | ||||
 | ||||
 Волна разряжения
Волна разряжения
 |


 Ударная волна
Ударная волна
 |


 Продукты детонации Р
Продукты детонации Р

 воздух
воздух
 |
Рис.21
На границе раздела имеет место перепад давления (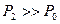 ) и находящиеся под большим давлением продукты детонации начнут быстро расширяться в сторону открытого торца заряда (в воздух). Приводя в движение и сжимая воздух продукты детонации образуют в нем ударную волну. Очевидно, что давление в продуктах детонации и в формируемой ударной волне (т.е. слева и справа от границы раздела) должны быть одинаковым. Так как в момент выхода детонационной волны на открытый торец заряда начинается расширение продуктов детонации, то вглубь их начнет распространяться волна разряжения. Скорость распространения фронта этой волны относительно продуктов детонации равна скорости звука в продуктах детонации. Она постепенно уменьшается от
) и находящиеся под большим давлением продукты детонации начнут быстро расширяться в сторону открытого торца заряда (в воздух). Приводя в движение и сжимая воздух продукты детонации образуют в нем ударную волну. Очевидно, что давление в продуктах детонации и в формируемой ударной волне (т.е. слева и справа от границы раздела) должны быть одинаковым. Так как в момент выхода детонационной волны на открытый торец заряда начинается расширение продуктов детонации, то вглубь их начнет распространяться волна разряжения. Скорость распространения фронта этой волны относительно продуктов детонации равна скорости звука в продуктах детонации. Она постепенно уменьшается от 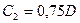 до
до 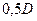 (в момент подхода к зоне покоя).
(в момент подхода к зоне покоя).
|
|
|
Определим скорость распространения границы раздела сред.
Эта скорость будет слагаться из скорости движения продуктов детонации за фронтом детонационной волны u2 и скорости истечения головных частей продуктов детонации u в момент выхода детонационной волны на поверхность заряда.
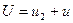
Уравнение состояния высоко нагретых и сильно сжатых газов подчиняется закону политропы
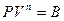 или
или 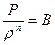
где n – показатель политропы.
Для политопного закона скорость движения расширяющихся газов записывается в виде
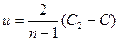
где 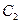 – скорость распространения звука в продуктах детонации к моменту выхода детонационной волны на поверхность заряда,
– скорость распространения звука в продуктах детонации к моменту выхода детонационной волны на поверхность заряда, 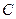 – скорость звука в воздухе, сжатом продуктами детонации до давления
– скорость звука в воздухе, сжатом продуктами детонации до давления 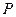 на границе раздела.
на границе раздела.
Скорость звука можно выразить через давление
Учитывая, что 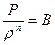
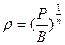
запишем 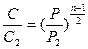
Подставляя значение 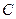 в выражение для скорости движения газов, получим
в выражение для скорости движения газов, получим
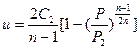
Если воспользоваться основными формулами гидродинамической теории детонации
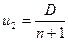 ,
, 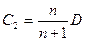 и зависимостью скорости движения газов можно
и зависимостью скорости движения газов можно
найти начальную скорость перемещения границы раздела сред.
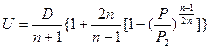
Как следует из этой формулы максимальная скорость истечения продуктов детонации 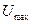 . соответствует случаю разлета в пустоту (
. соответствует случаю разлета в пустоту (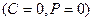 .
.
В этом случае ударной волны не образуется.
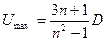
Если показатель политропы положить равным 3, то  , т.е. максимальная скорость разлета продуктов детонации равна скорости детонации.
, т.е. максимальная скорость разлета продуктов детонации равна скорости детонации.
Однако это противоречит опыту. Дело в том, что показатель политропы n = 3 справедлив только для сильно сжатых газов. При выходе газов на свободную поверхность давление в пустоте практически мгновенно падает до нуля. Так как зависимость 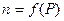 неизвестна, то полагают, что на каком-то этапе остается справедливым уравнение политропы (n = 3), а при падении давления ниже
неизвестна, то полагают, что на каком-то этапе остается справедливым уравнение политропы (n = 3), а при падении давления ниже 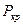 . расширение происходит по адиабатному закону
. расширение происходит по адиабатному закону 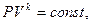 где
где 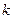 = 1,2.
= 1,2.
Найденные таким образом параметры ударных волн в воздухе, дают представление о параметрах продуктов детонации в момент их разлета с поверхности заряда (табл.18).
Таблица 18
 ВВ ВВ | 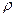 г/см3 г/см3 | 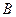 км/с км/с | 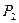 атм атм | 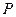 атм атм | 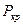 атм атм | 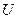 км/с км/с | 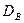 км/с км/с | 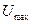 км/с км/с | 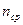 |
| Тротил | 1,6 | 7,0 | 6,45 | 7,1 | 10,5 | 2,20 | |||
| Гексоген | 1,6 | 8,2 | 7,45 | 8,2 | 11,9 | 2,24 |
где: 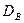 – начальная скорость ударной волны в воздухе;
– начальная скорость ударной волны в воздухе;
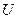 - скорость разлета продуктов детонации в воздухе;
- скорость разлета продуктов детонации в воздухе;
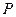 – начальное давление на границе раздела сред при разлете в возду- хе;
– начальное давление на границе раздела сред при разлете в возду- хе;
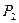 – давление на фронте детонационной волны.
– давление на фронте детонационной волны.
При разлете продуктов детонации в воздухе в связи с тем, что начальное давление 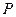 соизмеримо с
соизмеримо с 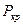 , на начальном этапе можно положить, что
, на начальном этапе можно положить, что
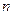 = 3 и величиной
= 3 и величиной 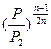 можно пренебречь (@ 0,1).
можно пренебречь (@ 0,1).
Следовательно, максимальная скорость истечения продуктов детонации в воздух равна 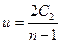 Отсюда при
Отсюда при 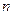 = 3
= 3 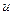 = C2, тогда
= C2, тогда 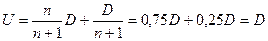
При определении скорости разлета с боковой поверхности заряда необходимо учитывать, что продукты детонации получили скорость 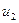 в направлении движения фронта детонации, а истечение их со скоростью
в направлении движения фронта детонации, а истечение их со скоростью 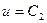 происходит перпендикулярно поверхности заряда (рис.22).
происходит перпендикулярно поверхности заряда (рис.22).

 C2 U
C2 U
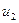



 U U
U U
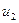
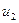

 C2 C2
C2 C2
Рис.22
С боковой поверхности U = 0,8D; с левого торца U = 0,5D.
По аналогии можно определить направление разлета продуктов детонации с заряда произвольной формы (рис.23).
 Взрывной луч С2
Взрывной луч С2



 U
U
Точка инициирования


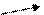
 u2
u2




 u2
u2
C2 U
Рис.23
|
|
|
 2015-07-14
2015-07-14 1189
1189