Параметры взрыва топливно-воздушных смесей в режиме детонации

1.2.1 Параметры детонации ТВС

Параметры на фронте детонационной волны в ТВС полностью определяются удельной теплотой взрыва смеси 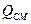, ккал/кг, показателем адиабаты продуктов взрыва 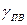, начальным давлением 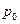, Па, и плотностью смеси 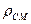, кг/м³.

;

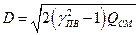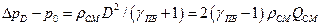(10)

,

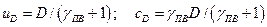где D - скорость распространения фронта детонационной волны (скорость детонации), м/с; 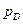, , 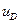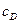- давление, Па, массовая скорость, м/с, и скорость звука, м/с, продуктов детонации на фронте волны.

Формулы (6.10), полученные для сильной детонационной волны, справедливы с погрешностью не более 5% при давлении на фронте 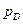>10 .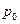

Плотность смеси связана с плотностью окружающего воздуха соотношением

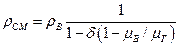(11)

где 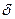= М_г / (М_в + М_г) - относительная массовая концентрация горючего; М_г, М_в - масса горючего и воздуха в смеси.

При использовании гетерогенных ТВС, то есть горючего в конденсированной фазе, 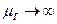. Тогда формула (11) принимает вид

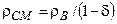
Удельная теплота взрыва Q_CM зависит от состава смеси и может быть рассчитана по удельной теплоте взрыва на единицу массы горючего Q_Г, если верно предположение, что в бедных ТВС реагирует вся масса топлива, а в богатых - лишь часть, соответствующая наличию кислорода в смеси. В этом случае нетрудно получить

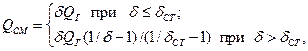(12)

где 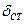- стехиометрическая концентрация.

Удельная теплота взрыва на единицу массы горючего определяется с помощью термодинамических расчетов. Кроме того, за 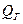можно принять стандартную теплоту сгорания горючего (табл. 1).

При известных теплоте взрыва и скорости детонации ТВС показатель адиабаты продуктов взрыва рассчитывается по формуле, являющейся следствием пеового соотношения (10)

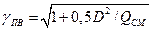. (13)

Анализ результатов термодинамических расчетов показывает, что показатель адиабаты продуктов взрыва принимает минимальное значение 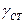при детонации ТВС стехиометрического состава и в первом приближении в области концентрационных пределов взрываемости смеси может быть описан линейной зависимостью

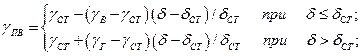(14)

где 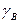=1,4 - показатель адиабаты воздуха; 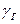- расчетная константа.

Для углеводородных газообразных и жидких топлив значения 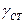и 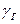меняются незначительно ( 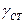= 1,23 ÷ 1,25; 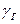= 1,5 ÷ 1,7) и могут быть приняты равными средним значениям 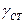= 1,24; 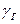= 1,6.

Для конденсированных горючих, остающихся в продуктах взрыва богатых ТВС в таком же состоянии, 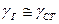. Например, при взрыве аэровзвеси пудры алюминия .

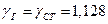При точечном источнике инициирования (взрыв заряда конденсированного ВВ, мощный искровой разряд и т.п.) формирующаяся детонационная волна обладает сферической симметрией (в ТВС с постоянной по объему концентрацией горючего) и параметры в продуктах взрыва за ее фронтом описываются автомодельным решением. В частности, для массовой и звуковой скоростей в продуктах взрыва справедливы соотношения

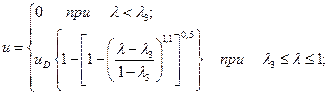(15)

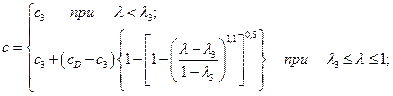(16)

где 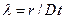- относительная координата за фронтом детонационной волны (r - расстояние от точки инициирования; t - время с момента начала инициирования), изменяющаяся от нуля в центре симметрии до единицы на фронте волны; 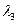, 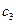- координата границы центральной области покоя и скорость звука в ней.

Две последние величины определяются по зависимости

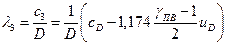, (17)

которую с учетом (10) можно переписать в виде

.

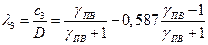Для смесей углеводородных топлив с воздухом. ( = 1,24) из последнего соотношения следует ; .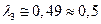

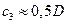Давление в продуктах взрыва за фронтом детонационной волны рассчитывается через скорость звука (6.16) по изоэнтропической зависимости

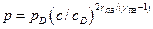(18)

Распределение давления p и массовой скорости и в продуктах взрыва за фронтом детонационной волны в стехиометрической углеводородной ТВС, построенные с использованием формул (15-18), приведены на рис. 1. Полагая, что r = const, t = var, можно построить зависимости p и u от времени в месте размещения объекта в области топливно-воздушной смеси, где на него не успевает оказывать влияние волна разрежения, приходящая от границы облака.

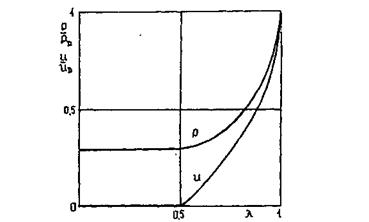
Рис. 1. Распределение давления(p) и массовой скорости (u) в продуктах взрыва за фронтом детонационной волны в стехиометрической углеводородной ТВС

6.1.2.2 Параметры детонационного взрыва внутри облака ТВС

Анализ результатов математического моделирования сферического взрыва газовых и гетерогенных ТВС показывает, что существуют две характерные области: внутри и вне смеси. Параметры в них зависят от соответствующих характеристик и меняются различным образом. При этом особое значение приобретают показатели на границе облака, связывающие поле взрыва обеих областей.

Начальное избыточное давление воздушной ударной волны 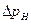может быть найдено из решения задачи о распаде произвольного разрыва. Учитывая относительно низкую интенсивность детонационной волны в ТВС, нетрудно получить приближенное аналитическое решение:

, (19)

где 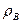- плотность воздуха, кг/м³.

Поскольку 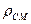мало отличается от 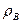, для стехиометрических углеводородных ТВС ( 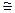1,24) соотношение (19) дает 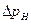= 0,78 .

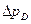Для удельного импульса избыточного давления на границе облака ТВС

,

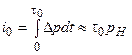где 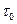- длительность фазы сжатия в волне, которая для сферической симметрии приблизительно равна 3,3 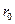/ D (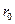 - радиус облака).

По результатам анализа численных результатов получено

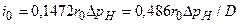. (20)

Для стехиометрических углеводородных ТВС (6.20) дает .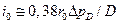

Максимальное избыточное давление 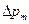внутри облака ТВС совпадает с избыточным давлением на фронте детонационной волны 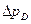и рассчитывается по соответствующему соотношению из (10).

Для удельного импульса избыточного давления вокруг места инициирования, учитывая автомодельное решение для сферической детонационной волны, может быть получена функциональная зависимость

,

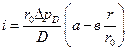где а, в - константы, которые по результатам численных расчетов равны 0,96 и 0,47. Следовательно,

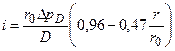(21)

В окрестности границы облака, за счет быстрого прихода волны разрежения, величина удельного импульса фазы сжатия может заметно отклоняться от зависимости (21). Обобщая эту формулу для всей области внутри ТВС, с учетом численных результатов можно записать

,

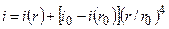где 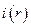и 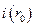- значения импульса, вычисленные по (21) для рассматриваемой точки 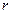границы облака .

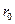С помощью (6.20), (6.21) последнее соотношение приводится к виду

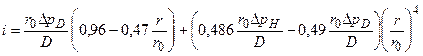. (22)

В случае применения стехиометрических углеводородных ТВС формула (22) упрощается и принимает вид

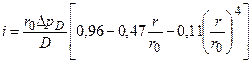
6.1.2.3 Параметры воздушной ударной волны при детонации ТВС

В качестве основных параметров, определяющих распространение взрывных волн, как правило, принимают энергию взрыва Е, а также давление 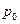и плотность 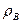окружающего воздуха. Однако физически более обоснованным является выбор не энергии взрыва, а энергии, уходящей в ударную волну 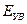(равна работе расширяющихся продуктов взрыва над окружающей средой).

При взрыве зарядов конденсированного ВВ энергия ударной волны составляет порядка 0,9 Е и слабо меняется при переходе от одного взрывчатого вещества к другому.

При детонации ТВС работа расширяющихся продуктов взрыва над окружающей атмосферой составляет примерно половину от выделившейся энергии Е и может заметно меняться в зависимости от состава смеси и параметров окружающего воздуха. Поэтому в качестве основного определяющего параметра ударных волн при детонации ТВС выбрана энергия ударной волны 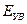, которую можно рассчитать по формуле

,

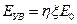где 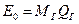- полная энергия, которая может выделиться при реагировании всей массы горючего; 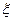- коэффициент полноты реакции горючего; 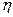- КПД взрыва, то есть отношение энергии, уходящей в ударную волну, к выделившейся при взрыве.

В случае идеальной детонации, то есть выделения всей энергии во фронте волны, в соответствии с (12) коэффициент полноты реакции горючего для ТВС с постоянной по объему концентрацией равен

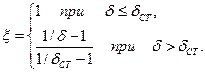(24)

Для типичных углеводородных ТВС на верхнем концентрационном пределе взрываемости коэффициент полноты реакции горючего составляет примерно 0,25; в плохоперемешанных смесях с областями концентрации горючего, выходящей за пределы взрываемости, - 0,02 ÷ 0,1.

КПД детонационного взрыва ТВС достаточно точно может быть рассчитан по формуле

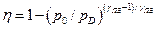, (25)

которая вытекает из модели равновесного расширения продуктов взрыва от детонационного давления до давления в окружающей атмосфере.

Для стехиометрических углеводородных ТВС с давлением на фронте детонационной волны 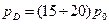значение КПД взрыва изменяется в диапазоне .

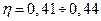Максимальное избыточное давление в точке, удаленной на расстояние r, м, от центра детонационного взрыва сферического облака ТВС, соответствует давлению на фронте ударной волны и рассчитывается по аппроксимационной зависимости

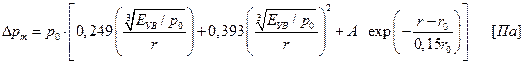(26)

Третье слагаемое в квадратной скобке (26) описывает очень резкий спад давления на фронте воздушной волны вблизи облака

ТВС и заметно влияет на результаты расчетов лишь при 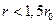. На больших расстояниях им можно пренебречь. Константа А определяется из (26) по известному начальному давлению ударной волны (19) при условии, что .

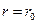Удельный импульс избыточного давления i фазы сжатия ударной волны на удалении r, м, от центра взрыва рассчитывается по формуле

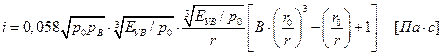. (27)

Выражение в квадратной скобке (27) описывает немонотонное изменение г в окрестности облака ТВС и при 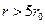становится практически равным единице. Константа В вычисляется по известному значению удельного импульса на границе облака ТВС (20) из (27) при 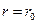. Для углеводородных ТВС на любых расстояниях (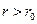) значение выражения в квадратных скобках отличается от единицы не более чем на 10%. Поэтому с указанной погрешностью для оценки удельного импульса воздушной ударной волны можно воспользоваться зависимостью

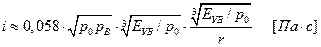. (28)

Запись выражений для определения максимального избыточного давления и удельного импульса (26-28) с использованием 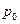позволяет учесть влияние давления окружающей атмосферы (при взрывах на различной высоте над уровнем моря), а введение 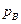в формулы для расчета удельного импульса дает возможность также учитывать температуру и влажность воздуха.

В случае формирования облака ТВС непосредственно у поверхности земли в первом приближении его можно представить в виде полусферического объема. При этом в зависимости (26-28) следует подставлять удвоенную энергию ударной волны, рассчитанную по соотношению (23), а радиус облака 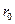- вычислять как для полусферы.