Стационарный режим распространения детонации

Достаточно сильная ударная волна может вызвать воспламенение на-гретой ею взрывчатой среды. Однако горение, вызванное одиночным импуль-сом сжатия, может быть нестационарным. При одиночном, впоследствии за-тухающем импульсе сжатия воспламенение нагретого газа может иницииро-вать дефлаграционное горение. Ударная волна создает неизменные условия сжатия все новых слоев газа только в том случае, если ее поддерживать внешним воздействием, например, непрерывным движением сжимающего поршня.

Расширение газа при его сгорании само может приводить к сжатию и нагреванию новых, еще холодных слоев взрывчатой среды и ее воспламене-нию. Расширяющиеся продукты реакции играют роль сжимающего поршня. Возникает комплекс из ударной волны, бегущей по взрывчатой среде, и сле-дующей за нею зоны быстрой реакции в газе, нагретом ударной волной. Теп-ловыделение в этой зоне поддерживает устойчивое существование ударной волны. Такой комплекс, именуемый детонационной волной, стационарен, т.е. распространяется на неограниченном протяжении без изменения его струк-туры.

При детонационном горении от слоя к слою передается лишь импульс сжатия, - теплопроводность в этом процессе не играет роли. Детонационная волна распространяется со скоростью порядка нескольких километров в се-кунду. Давление в ней в несколько раз превосходит максимальное давление адиабатического сгорания в замкнутом сосуде, и потому детонация может вы-звать большие разрушения. Так как скорость детонации больше скорости зву-ка и никакое возмущение в газе не может опередить детонационную волну, то разрушающее действие волны не зависит от того, возникает ли детонация в открытом или закрытом сосуде.

Отличительную особенность детонации представляет ее строгая ста-ционарность. В достаточно широких длинных трубах детонация распростра-няется с неизменной скоростью, которая не зависит от аппаратурных условий и давления и лишь слабо зависит от начальной температуры. Скорость дето-нации зависит только от термодинамических характеристик газовой смеси. Другая особенность детонационного горения заключается в том, что при де-тонации продукты реакции движутся в ту же сторону, что и зона реакции, то-гда как при дефлаграции эти направления противоположны. Лишь впоследст-вии, после подхода волны разрежения, величина скорости продуктов реакции меняет знак на обратный.

Скачок давления в ударной волне происходит на расстоянии длины свободного пробега молекул, но химическая реакция, даже высокотемпературная, протекает только после многих столкновений. По этой причине, а также вследствие большой скорости детонационной волны ширина зоны реакции достаточно велика.

Уравнение (8.4) справедливо для любых систем. В любой точке зоны реакции стационарной детонационной волны соблюдается зависимость

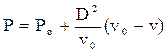, (8.4а)

описывающая (в Р – vкоординатах) (рис. 34) так называемую прямую Ми-хельсона – одного из создателей теории детонации.

Обозначим индексами 0, 1 и 2 соответственно состояния газа до сжатия в ударной волне, непосредственно после сжатия, но до начала реакции, и по-сле завершения реакции.

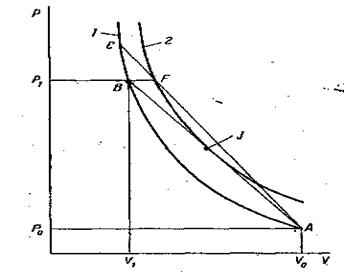
Рис. 34. Изменение состояния газа при детонации.

8.5. Определение скорости детонации.

Нанесем на график (рис. 34) две адиабаты Гюгонио: для исходной сре-ды 1и для сжатых продуктов реакции 2.Адиабата 2не проходит через точку исходного состояния Р_о, v_о,как адиабата 1; последнее очевидно из уравнения (8.10): при v₁ = v_о, Р_i = Р₂. Для адиабаты 2уравнение (8.6) по-прежнему спра-ведливо, однако условие (8.9) выполняется только для продуктов реакции, а для исходной среды должно быть заменено на

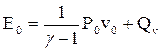(8.9а)

где: Q_v– теплота сгорания единицы массы. Подстановка значений Е и Е_о в уравнение (8.6) дает при v₂ = v_о:

Р₂ = Р_о + Q (g — 1)/v_о. (8.24)

По этой причине вся адиабата 2располагается выше адиабаты 1. На-клон прямой Михельсона определяет скорость детонации: она тем выше, чем круче поднимается прямая. Очевидно, что эта прямая не может целиком раз-мещаться ниже адиабаты 2,так как в этом случае стационарное распростра-нение детонационной волны не приводило бы к образованию продуктов сго-рания.

Устойчивая детонация возможна только в том случае, когда адиабата 2 касается прямой Михельсона. Этот режим соответствует наименьшей воз-можной скорости детонации. В точке касания J, именуемой точкой Жуге, за-вершается переход исходного газа в продукты сгорания, а значит, и тепловы-деление. Поскольку реакция в горящем газе необратима, энтропия возрастает при изменении состояния вдоль прямой (8.4а) в направлении к точке Р_о, v_о. В точке Jреакция завершается, dQ = TdS = 0, а значит, dS = 0, энтропия дости-гает максимума.

Учитывая уравнение (8.19), запишем

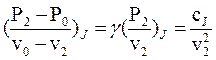(8.25)

где: с_J– скорость звука в продуктах сгорания при состоянии, отвечающем точке Жуге. Из уравнений (8.1), (8.4) и (8.3) следует, что

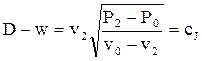(8.26)

т.е. скорость детонации по отношению к продуктам сгорания равна скорости распространения в них звука (до начала расширения), а по отношению к го-рючей среде – сумме скорости звука в продуктах реакции и скорости их дви-жения.

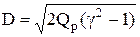(8.27)

Из уравнения (8.27) следует, что скорость детонации определяется тер-модинамическими свойствами вещества и зависит лишь от калорийности го-рючей среды в расчете на единицу массы и отношения теплоемкостей. Урав-нение поясняет экспериментально установленные факты: скорость детонации практически не зависит от давления и начальной температуры.

Другая особенность детонационного сгорания, как следует из уравне-ния (8.27), заключается в характере влияния состава на скорость детонации. Так, стехиометрическая смесь 2Н₂ + О₂, разбавляемая азотом, детонирует с большей скоростью, чем та же смесь, разбавленная таким же количеством ки-слорода (т.е. одним из реагирующих компонентов), ввиду меньшего молеку-лярного веса азота. Разбавление смеси 2Н₂ + О₂ избыточным водородом за-метно увеличивает скорость детонации. Несмотря на понижение температуры горения, действие такой добавки ускоряет детонацию вследствие уменьшения среднего молекулярного веса смеси.

Давление в детонационной волне вдвое превосходит равновесное дав-ление взрыва в замкнутом объеме. Отражение от препятствия ударной волны, возникающей при детонации, приводит к дополнительному росту давления в соответствии с уравнением (8.23). Эти соотношения показывают, как велика сила разрушительного действия детонационной волны.