Принцип действия основан на взаимодействии магнитных полей неподвижной и подвижной катушек, по которым протекают измеряемые токи.
 |
Рис.7
Уравнение шкалы выводится аналогичным образом из условия равновесия 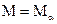 .
.
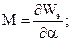
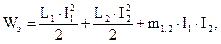 где
где 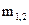 - взаимная индуктивность между катушками. Рассмотрим несколько случаев.
- взаимная индуктивность между катушками. Рассмотрим несколько случаев.
1. Оба протекающих тока являются постоянными, т.е. 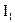 и
и 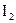 - const. Тогда
- const. Тогда 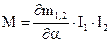 , а
, а 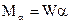 . Отсюда можно получить уравнение шкалы прибора
. Отсюда можно получить уравнение шкалы прибора
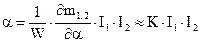 .
.
Таким образом, характер шкалы прибора электродинамической системы неравномерный при 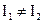 . При
. При 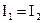 характер шкалы квадратичный.
характер шкалы квадратичный.
2. При измерении в цепях переменного тока 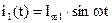 и
и 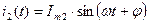 подвижная часть прибора будет реагировать на среднее значение вращающего момента
подвижная часть прибора будет реагировать на среднее значение вращающего момента
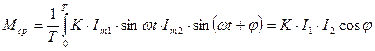 .
.
Из формул следует, что показания приборов ЭД системы пропорциональны произведению токов, а градуировка шкалы справедлива как для постоянных величин, так и для переменных.
Достоинства
1. Могут иметь высокий класс точности (до 0,2).
2. Обеспечивают перемножение измеряемых величин, т.е. при последовательно-параллельном включении можно измерять мощность.
 |
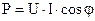
Недостатки
1. Малая чувствительность.
2. Нелинейность шкалы.
3. Большие габариты и сложность конструкции.
4. Плохая защищённость от влияния внешних магнитных полей, температуры, частоты.
5. Недопустимость перегрузок.
6. Низкий частотный диапазон (1,5  3кГц).
3кГц).
Область применения
 Используются в качестве амперметров (до 200А), вольтметров (до600В), ваттметров (до 1,5кВт). Могут служить образцовыми приборами при градуировке рабочих приборов. Для увеличения чувствительности неподвижная катушка заключается в магнитомягкий магнитопровод. Такой прибор называется прибором ферродинамической системы и обозначается.
Используются в качестве амперметров (до 200А), вольтметров (до600В), ваттметров (до 1,5кВт). Могут служить образцовыми приборами при градуировке рабочих приборов. Для увеличения чувствительности неподвижная катушка заключается в магнитомягкий магнитопровод. Такой прибор называется прибором ферродинамической системы и обозначается.
В заключение приведем сводную таблицу уравнений шкал измерительных механизмов различных систем.
| Система прибора | Уравнение шкалы | Значение сигнала, измеряемое прибором (отклик). |
 | 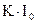 | Постоянная составляющая |
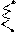 | 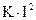 | Среднеквадратическое |
 | 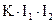 , если , если 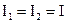 то то 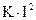 | Среднеквадратическое |
 | 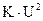 | Среднеквадратическое |
 2015-07-14
2015-07-14 1287
1287








