Доказательство

Теорема Минца об устойчивости конструктивной истинности.

Операции редукции.

1.

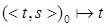
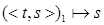
2.

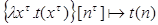
^3.

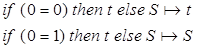
4.

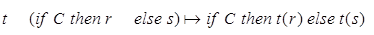
Редуцирование за несколько шагов.

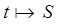за несколько шагов,если существуют 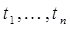, такие что

.

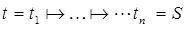Теорема (Г.Е. Минц).

Пусть ├_скип → F и ей по теореме Клини-Нельсона соответствует терм t^F.

Пусть к этому доказательству применяется процедура устранения сечения и новому доказательству (без сечений) соответствует терм S^F.

Тогда t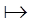^F S^F.

Доказательство.

Комбинация теоремы об устранении сечения и теоремы Клини-Нельсона.

Рассмотрим случаи:

1.С – не является главной в левой посылке.

2.С – не является главной в правой посылке.

3.С - главная формула в обеих посылках.

1.

1) удаление &:

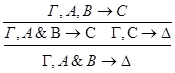
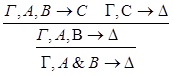
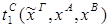
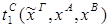
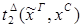
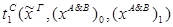
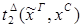
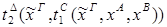
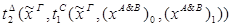
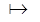
2)удаление Ú:

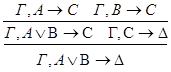
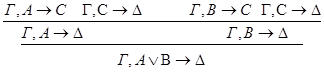
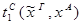
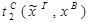
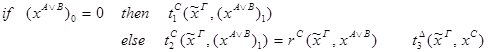
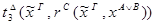
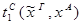
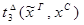
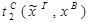
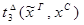
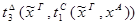
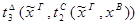
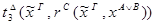
3) удаление :

) )

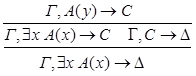
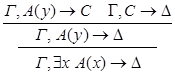
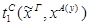
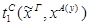
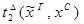
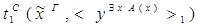
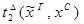
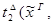
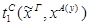
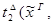
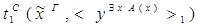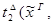
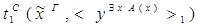4) удаление :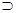

)

) )

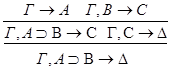
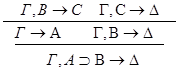
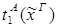
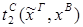
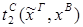
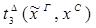
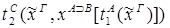
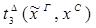
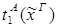
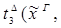
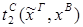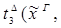
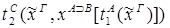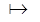
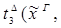
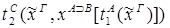1) удаление :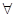

)

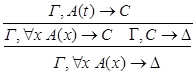
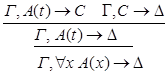
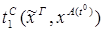
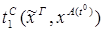
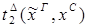
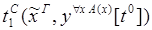
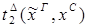
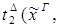
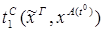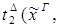
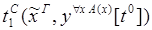
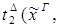
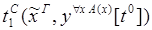
2.

1)введение &:

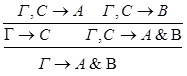
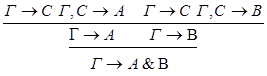
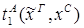
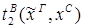
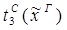
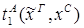
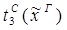
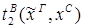
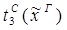
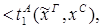
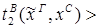
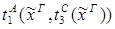
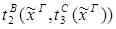
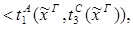
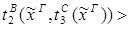
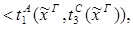
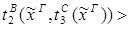
2)удаление &:

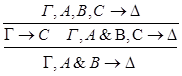
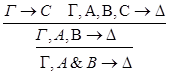
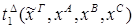
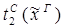
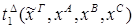
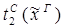
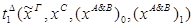
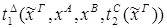
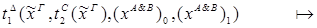
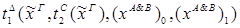
2) введение Ú:

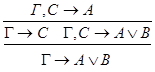
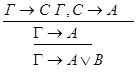
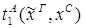
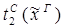
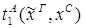
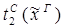
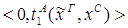
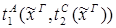
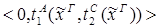
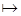
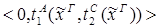
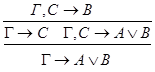
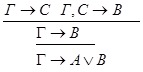
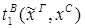
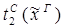
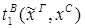
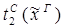
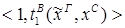
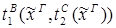
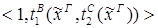
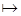
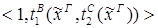
4) удаление Ú:

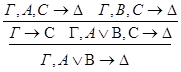
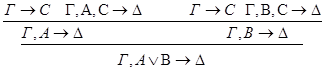
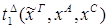
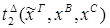
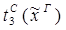
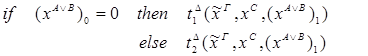
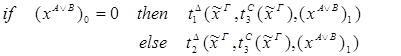
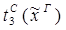
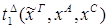
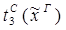
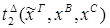
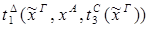
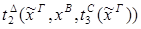
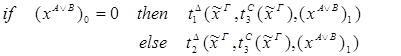
5) введение :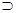

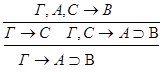
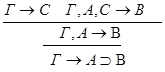
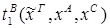
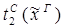
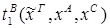
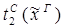
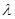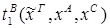
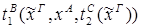
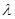x^А.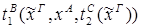

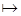
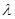x^А. x^А.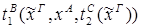

6) удаление :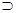

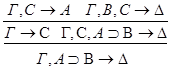
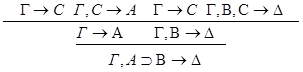
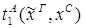
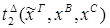
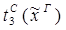
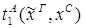
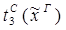
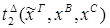
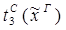
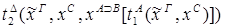
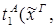
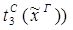
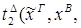
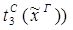
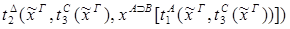
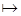
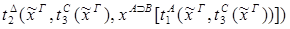
6) введение :

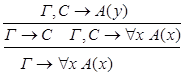
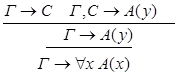
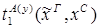
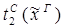
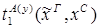
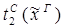
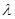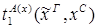
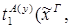
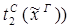
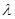x.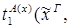

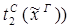
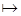
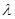x. x.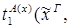

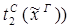
8) удаление :

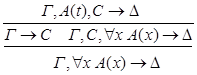
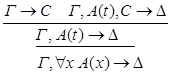
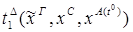
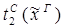
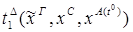
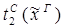
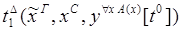
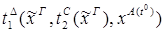
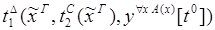
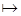
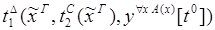
9) введение :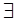

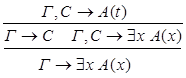
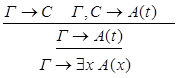
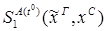
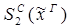
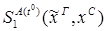
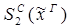
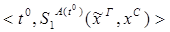
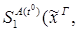
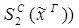
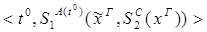
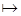
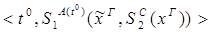
10) удаление :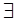

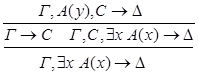
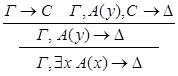
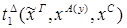
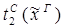
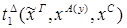
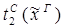
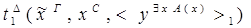
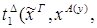
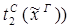
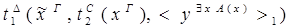
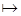
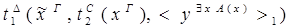
3.

1)&

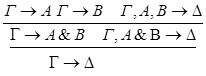
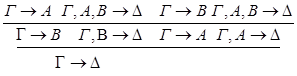
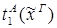
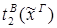
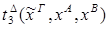
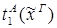
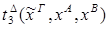
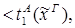
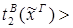
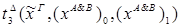
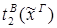
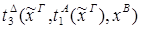
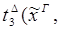
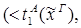
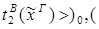
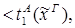
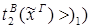
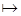
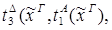
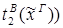
редуцируется за 2 шага

2) Ú

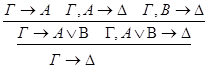
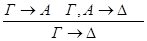
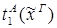
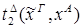
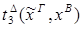
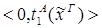
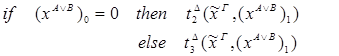
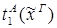
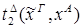
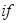
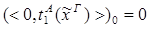
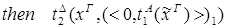
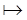
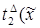
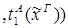
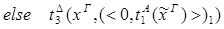
редуцируется за 3 шага

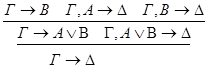
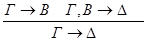
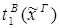
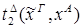
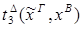
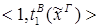
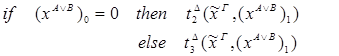
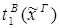
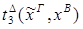
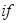
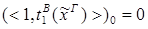
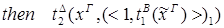
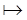
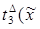
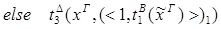
редуцируется за 3 шага

3) :

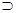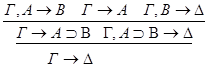
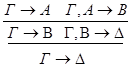
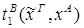
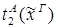
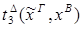
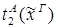
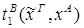
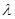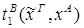
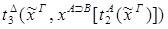
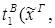
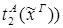
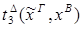
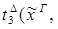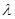x^А.

{ x^А. }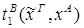

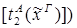
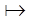
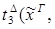
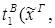
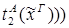
редуцируется за 1 шаг

4) :

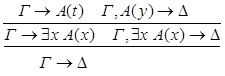
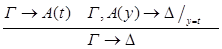
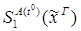
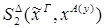
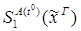
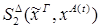
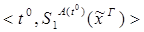
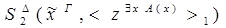
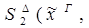
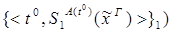
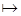
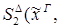
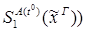
редуцируется за 1 шаг

5) :

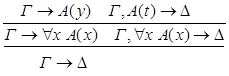
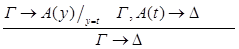
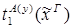
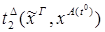
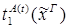
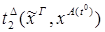
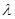x.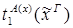

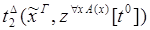
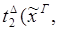
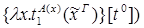
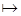
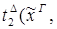
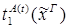
редуцируется за 1 шаг

Теорема доказана полностью.