2015-07-14
442
Непротиворичивость СКИВ относительно семантики Крипке.
Теорема.
Если формула доказуема в СКИВ, то она является тождественно истинной по Крипке.
├скив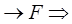 
╞Крипке 
.
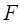Доказательство.
Пусть секвенция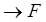 
доказуема в СКИВ.
Рассмотрим доказательство секвенции :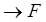
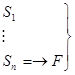(1)
Докажем, что каждая из секвенций данного доказательства тождественно истинна по Крипке.
Доказательство проведём по индукции.
Заметим, что секвенция Г→∆ опрвержима по Крипке, если существует интерпретация КрипкеK=<W, w0, R,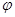 
>, в которой все формулы из Г истинны, а формула ∆ ложна.
n =1. Секвенция имеет вид А→А.
Предположим, что она опровержима по Крипке.Пусть K=<W, w0, R, 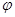> - интерпретация Крипке, в которой А истинна и А ложна. Чего не может быть.
Пусть теорема верна для всех n<k. Докажем для n=k.
Последняя секвенция Г→∆ выводится по одному из правил вывода.
Рассмотрим 6 возможных случаев.
1) введение &
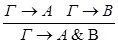
По индукционному предположению,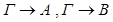 
общезначимы по Крипке. Предположим, что секвенция-заключение 
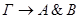опровержима по Крипке. Тогда существует интерпретация Крипке K=<W, w0, R, 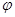>, где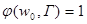 
|
|
|
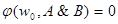
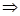
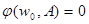или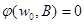 
.
Отсюда следует, что секвенция
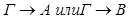опровержима по Крипке. Это противоречит нашему индукционному предположению.
Значит, секвенция Г→ A&B общезначима по Крипке.
2)удаление &
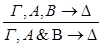
По индукционному предположению,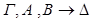 
общезначима по Крипке. Пусть секвенция-заключение 
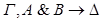опровержима по Крипке. Тогда существует интерпретация Крипке K=<W, w0, R, 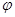>, где
, 
, 
.
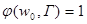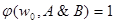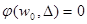
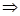
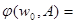
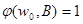Отсюда следует, что 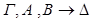опровержима по Крипке.
Это противоречит нашему индукционному предположению.
Значит, секвенция 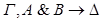общезначима по Крипке.
3) введение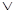 
а)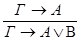 
б)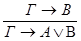 
а). По индукционному предположению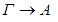 
общезначима по Крипке. Пусть секвенция- заключение 
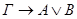опровержима по Крипке. Тогда существует модель Крипке K=<W, w0, R, 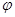>, где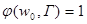
.
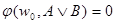
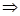
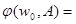
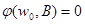Отсюда следует, что 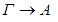опровержима по Крипке.
Это противоречит нашему индукционному предположению.
Значит, секвенция 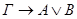общезначима по Крипке.
б). Полностью аналогично.
4)удаление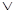
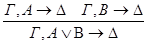
По индукционному предположению секвенции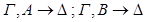 
общезначимы по Крипке. Пусть секвенция-заключение 
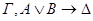опровержима по Крипке. Тогда существует модель Крипке K=<W, w0, R, 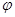>, где ,
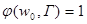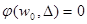
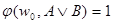
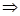
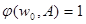или .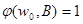
Отсюда следует, что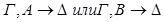 
опровержима по Крипке.
Это противоречит нашему индукционному предположению.
Значит, секвенция 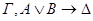общезначима по Крипке.
5) удаление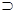 
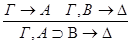
По индукционному предположению секвенции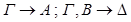 
общезначимы по Крипке. Пусть секвенция-заключение 
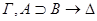опровержима по Крипке. Тогда существует модель Крипке K=<W, w0, R, 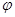>, где ,
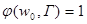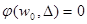
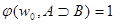
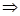
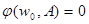или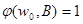
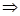
используя свойство рефлексивности отношения R, заключаем, что одна из секвенций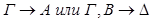 
опровержима по Крипке.
Это противоречит нашему индукционному предположению.
|
|
|
Значит, секвенция 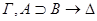общезначима по Крипке.
6) введение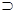
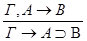
По индукционному предположению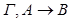 
общезначима по Крипке.
Пусть секвенция-заключение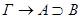 
опровержима по Крипке. Тогда существует модель Крипке K=<W, w0, R, 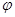>, где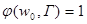 
.
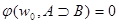Следовательно, существует мир w, достижимый из w0, где А принимает значение1, В принимает значение 0. Какое значение принимают формулы из Г в мире w? Покажем, что все они истинны в w. (Отсюда будет следовать, что секвенция 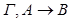опровержима по Крипке. Это противоречит нашему индукционному предположению. Значит, секвенция 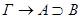будет общезначима по Крипке.)
Для этого докажем лемму о монотонности.
Лемма. Пусть К – произвольная модель Крипке, w – произвольный мир и u – произвольный мир, достижимый из w. Пусть F – произвольная формула. Тогда если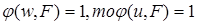 
Доказательство.
Доказываем индукцией по сложности формулы F (m- число логических связок в F).
m=0.
Тогда F – элементарная переменная. Утверждение леммы следует из свойства монотонности разметки интерпретаций Крипке для КИВ.
Пусть лемма справедлива для m<k. Докажем для m=k. Рассмотрим главную связку F.
а) F=A&B
В мире w F=1 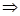A=B=1. Тогда по индукционному предположению в мире u А=В=1. Следовательно, F=1 в мире u.
b) F=A 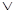B
В мире w F=1 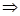A=1 или B=1. Тогда по индукционному предположению в мире u А=1 или В=1. Следовательно, F=1 в мире u.
c) F=A 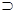B
В мире w F=1. Докажем, что в мире u также F=1.
Доказательство от противного. Пусть F=0 в мире u, т.е. существует мир v, достижимый из u, где А=1, В=0. Но по свойству транзитивности мир v достижим и из w тоже. Т.е. в мире w истинностное значение F должно равняться 0. Противоречие. Значит F=1 в мире u. Лемма доказана полностью.
Доказательство теоремы о непротиворечивости закончено.
